设A(xA,yA),B(xB,yB)为平面直角坐标系上的两点,其中xA,yA,BxB,yB∈Z.令△x=xB-xA,△y=yB-yA,若|△x|+|△y=3,且|△x|-|△y|≠0,则称点B为点A的“相关点”,记作:B=i(A).
(Ⅰ)请问:点(0,0)的“相关点”有几个?判断这些点是否在同一个圆上,若在,写出圆的方程;若不在,说明理由;
(Ⅱ)已知点H(9,3),L(5,3),若点M满足M=i(H),L=i(M),求点M的坐标;
(Ⅲ)已知P0(x0,y0)(x0∈Z,Y0∈Z)为一个定点,点列{Pi}满足:Pi=i(Pi-1),其中i=1,2,3,…,n,求|P0Pn|的最小值.
解:(I)因为|△x|+|△y=3,且|△x|-|△y|≠0,|△x|与|△y|为非零整数,
故|△x|=1,|△y|=2;或|△x|=2,|△y|=1,所以点(0,0)的“相关点”有8个,
分别为:(1,2)、(1,-2)、(-1,2)、(-1,-2)、(2,1)、(2,-1)、
(-2,1)、(-2,-1).…(1分)
又因为 (△x)
2+(△y)
2=5,即
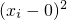
+
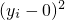
=5,
所以,这些可能值对应的点在以(0,0)为圆心,以

为半径的圆上.…(3分)
(II)设M(x
M,y
M),因为M=i(H),L=i(M),
所以有|x
M-9|+|y
M-3|=3,|x
M-5|+|y
M-3|=3,…(5分)
所以|x
M-9|=|x
M-5|,所以x
M=7,故y
M=2 或 y
M=4,
所以M(7,2),或M(7,4).…(7分)
(III)当n=2k,且 k∈N
* 时,|P
0P
n|的最小值为0.例如:P
0(x
0,y
0 ),
P
1 (x
0+1,y
0 ),P
2((x
0,y
0 ),显然,P
0=i(P
1),P
1=i(P
2),此时,|P
0P
2|=0.…(8分)
当n=1时,可知,|P
0P
n|的最小值为

.…(9分)
当n=3 时,对于点P,按照下面的方法选择“相关点”,可得P
3(x
0,y
0+1):
由P
0(x
0,y
0 ),依次找出“相关点”分别为P
1(x
0+2,y
0+1),P
2(x
0+1,y
0+3),P
3(x
0,y
0+1).
此时,|P
0P
3|=1,故|P
0P
n|的最小值为1.…(11分)
然后经过3次变换回到P
3(x
0,y
0+1),故|P
0P
n|的最小值为1.
当n=2k+1,k>1,k∈N
* 时,经过2k次变换回到初始点P
0(x
0,y
0 ),
故经过2k+1次变换回到P
3(x
0,y
0+1),故|P
0P
n|的最小值为1.
综上,当 n=1 时,|P
0P
n|的最小值为

.
当当n=2k,k∈N
* 时,|P
0P
n|的最小值为0,
当n=2k+1,k∈N
* 时,|P
0P
n|的最小值为1. …(13分)
分析:(I)由题意可得|△x|=1,|△y|=2;或|△x|=2,|△y|=1,由此可得点(0,0)的“相关点”有8个.再根据
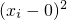
+
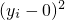
=5,可得这些可能值对应的点在以(0,0)为圆心,以

为半径的圆上.
(II)设M(x
M,y
M),由条件推出|x
M-9|+|y
M-3|=3,|x
M-5|+|y
M-3|=3,由此求得点M的坐标.
(III) 分当n=1、当n=2k,当n=2k+1,且 k∈N
* 时,三种情况,分别求得|P
0P
n|的最小值,综合可得结论.
点评:本题主要考查圆的方程,两点间的距离公式,体现了分类讨论的数学思想,属于中档题.

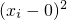 +
+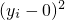 =5,
=5, 为半径的圆上.…(3分)
为半径的圆上.…(3分) .…(9分)
.…(9分) .
.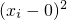 +
+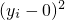 =5,可得这些可能值对应的点在以(0,0)为圆心,以
=5,可得这些可能值对应的点在以(0,0)为圆心,以 为半径的圆上.
为半径的圆上.


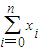 ,求T的最大值.
,求T的最大值.