
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() .若对任意的
.若对任意的![]() ,
,![]() ,都有
,都有![]() .
.
(1)判断函数![]() 的单调性,并说明理由;
的单调性,并说明理由;
(2)若![]() ,求实数
,求实数![]() 的取值范围;.
的取值范围;.
(3)若不等式![]() 对任意
对任意![]() 和
和![]() 都恒成立,求实数
都恒成立,求实数![]() 的取值范围.
的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】随着电商的快速发展,快递业突飞猛进,到目前,中国拥有世界上最大的快递市场.某快递公司收取快递费的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,在收费10元的基础上,每超过
的包裹,在收费10元的基础上,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收5元.
计算)需再收5元.
该公司将最近承揽的100件包裹的重量统计如下:

公司对近60天,每天揽件数量统计如下表:

以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来5天内恰有2天揽件数在101~300之间的概率;
(2)①估计该公司对每件包裹收取的快递费的平均值;
②根据以往的经验,公司将快递费的三分之一作为前台工作人员的工资和公司利润,其余的用作其他费用.目前前台有工作人员3人,每人每天揽件不超过150件,日工资100元.公司正在考虑是否将前台工作人员裁减1人,试计算裁员前后公司每日利润的数学期望,若你是决策者,是否裁减工作人员1人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1,2),点M的极坐标为 ![]() ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为 ![]() ,圆C以M为圆心,3为半径.
,圆C以M为圆心,3为半径.
(1)求直线l的参数方程和圆C的极坐标方程;
(2)设直线l与圆C相交于A,B两点,求|PA||PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率
的离心率![]() .
.
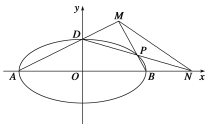
(1)求椭圆![]() 的方程;
的方程;
(2)如图所示,A、B、D是椭圆C的顶点,P是椭圆C上除顶点外的任意一点,直线DP交x轴于点N,直线AD交BP于点M,设BP的斜率为k,MN的斜率为m.证明:2m-k为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() 是某公共汽车线路收支差额
是某公共汽车线路收支差额![]() 元与乘客量
元与乘客量![]() 的图象.由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的方案,根据图
的图象.由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的方案,根据图![]() 上点
上点![]() 、点
、点![]() 以及射线
以及射线![]() 上的点的实际意义,用文字说明图
上的点的实际意义,用文字说明图![]() 方案是______,图
方案是______,图![]() 方案是______.
方案是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足f(﹣x)=f(x),且当x<0,f(x)=3x+1,若a= ![]() ,b=
,b= ![]() ,c=2
,c=2 ![]() ,则有( )
,则有( )
A.f(a)<f(b)<f(c)
B.f(b)<f(c)<f(a)
C.f(b)<f(a)<f(c)
D.f(c)<f(a)<f(b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com