Question

已知定义在R上的偶函数g（x）满足：当x≠0时，xg′（x）＜0（其中g′（x）为函数g（x）的导函数）；定义在R上的奇函数f（x）满足：f（x+2）=-f（x），在区间[0，1]上为单调递增函数，且函数y=f（x）在x=-5处的切线方程为y=-6．若关于x的不等式g[f（x）]≥g（a²-a+4）对x∈[6，10]恒成立，则a的取值范围是（ ）
A．-2≤a≤3
B．a≤-1或a≥2
C．-1≤a≤2
D．a≤-2或a≥3

Answer 1

【答案】分析：根据“xg′（x）＜0”和导数与函数单调性的关系，判断出函数g（x）的单调性，再将“g[f（x）]≥g（a²-a+4）对x∈[6，10]恒成立”，转化为“|f（x）|≤|a²-a+4|对x∈[6，10]恒成立”，再由条件求出函数f（x）的周期、对称轴以及f（-5）的值，再得f（-1）、f（1）、f（3）的值，再由这些性质画出大致图象，右图象求出函数f（x）在[6，10]上的值域，从而求出最大值，列出关于a的不等式求解．
解答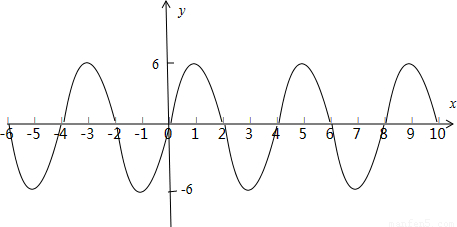：解：∵当x≠0时，xg′（x）＜0，∴当x＞0时，g′（x）＜0，当x＜0时，g′（x）＞0，
即g（x）在（-∞，0）上递增，在（0，+∞）上递减，
∵不等式g[f（x）]≥g（a²-a+4）对x∈[6，10]恒成立，
∴|f（x）|≤|a²-a+4|对x∈[6，10]恒成立，
由f（x+2）=-f（x）得，f（x+4）=-f（x+2）=f（x），则函数f（x）是以4为周期的周期函数，
又∵f（x）是R上的奇函数，∴f（x+2）=-f（x）=f（-x），则函数f（x）的对称轴是x=1，
∵在x=-5处的切线方程为y=-6，∴f（-5）=-6，即f（-1）=f（3）=-6，f（1）=6，
再结合f（x）在区间[0，1]上为单调递增函数，且f（0）=0，画出大致图象：
由上图得，当x∈[6，10]时，f（x）∈[-6，6]，
由|f（x）|≤|a²-a+4|对x∈[6，10]恒成立，得6≤|a²-a+4|，
即a²-a+4≥6或a²-a+4≤-6，化简得a²-a-2≥0或a²-a+10≤0，
解得a≤-1或a≥2，
故选B．
点评：本题是有关函数性质的综合题，考查了导数与函数单调性的关系，函数的奇偶性与单调性关系、对称性、周期性等，考查了转化思想和数形结合思想，难度以及综合程度都很大．