
已知定义在R上的二次函数R(x)=ax2+bx+c满足![]() ,且R(x)的最小值为0,函数h(x)=lnx,又函数f(x)=h(x)-R(x).
,且R(x)的最小值为0,函数h(x)=lnx,又函数f(x)=h(x)-R(x).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)当a≤![]() 时,若x0∈[1,3],求f(x0)的最小值;
时,若x0∈[1,3],求f(x0)的最小值;
(Ⅲ)若二次函数R(x)图象过(4,2)点,对于给定的函数f(x)图象上的点A(x1,y1),当![]() 时,探求函数f(x)图象上是否存在点B(x2,y2)(x2>2),使A、B连线平行于x轴,并说明理由.(参考数据:e=2.71828…)
时,探求函数f(x)图象上是否存在点B(x2,y2)(x2>2),使A、B连线平行于x轴,并说明理由.(参考数据:e=2.71828…)
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | e |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三第二次质检理科数学复习卷(二) 题型:解答题
.已知定义在R上的二次函数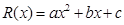 满足
满足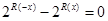 ,且
,且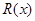 的最小值
的最小值
为0,函数 ,又函数
,又函数 。
。
(I)求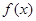 的单调区间; (II)当
的单调区间; (II)当 ≤
≤ 时,若
时,若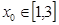 ,求
,求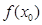 的最小值;
的最小值;
(III)若二次函数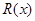 图象过(4,2)点,对于给定的函数
图象过(4,2)点,对于给定的函数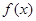 图象上的点A(
图象上的点A( ),
),
当 时,探求函数
时,探求函数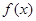 图象上是否存在点
图象上是否存在点 (
( )(
)(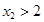 ),使
),使 、
、 连线平行于
连线平行于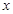 轴,并说明理由。(参考数据:e=2.71828…)
轴,并说明理由。(参考数据:e=2.71828…)
查看答案和解析>>
科目:高中数学 来源:2012届山东省日照市高三上学期测评理科数学试卷 题型:解答题
已知定义在R上的二次函数 满足
满足 ,且
,且 的最小值为0,函数
的最小值为0,函数 ,又函数
,又函数 。
。
(I)求 的单调区间;
的单调区间;
(II)当 ≤
≤ 时,若
时,若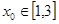 ,求
,求 的最小值;
的最小值;
(III)若二次函数 图象过(4,2)点,对于给定的函数
图象过(4,2)点,对于给定的函数 图象上的点A(
图象上的点A( ),当
),当 时,探求函数
时,探求函数 图象上是否存在点B(
图象上是否存在点B( )(
)(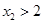 ),使A、B连线平行于x轴,并说明理由。
),使A、B连线平行于x轴,并说明理由。
(参考数据:e=2.71828…)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com