
����Ŀ����ͼ���ҹ�2008����2014������������������������λ���ڶ֣�������ͼ 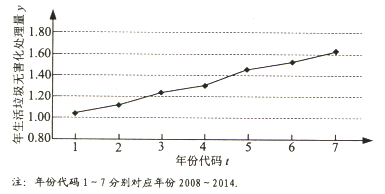
����������ͼ�������������Իع�ģ�����y��t�Ĺ�ϵ���������ϵ������˵����
������y����t�Ļع鷽�̣�ϵ����ȷ��0.01����Ԥ��2017���ҹ���������������������
�ο����ݣ� ![]() =9.32��
=9.32�� ![]() yi=40.17��
yi=40.17�� ![]() =0.55��
=0.55�� ![]() ��2.646��
��2.646��
�ο���ʽ�����ϵ��r= 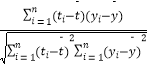 �ع鷽��
�ع鷽�� ![]() =
= ![]() +
+ ![]() t ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
t ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ�� ![]() =
= 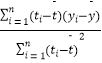 ��
�� ![]() =
= ![]() ��
�� ![]() ��
��
���𰸡��⣺����������ͼ������y��t֮����ڽ�ǿ������ع�ϵ���� ![]() =9.32��
=9.32�� ![]() yi=40.17��
yi=40.17�� 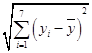 =0.55��
=0.55��
��r�� ![]() ��0.993��
��0.993��
��0.993��0.75��
��y��t֮����ڽ�ǿ������ع�ϵ��
������ ![]() ��1.331������
��1.331������ ![]() =
= ![]() ��0.103��
��0.103��![]() =1.331��0.103��4=0.92��
=1.331��0.103��4=0.92��
���ԣ�y����t�Ļع鷽��Ϊ�� ![]() =0.92+0.10t��
=0.92+0.10t��
��2017���Ӧ��t=10����ع鷽�̵ã� ![]() =0.92+0.10��10=1.92
=0.92+0.10��10=1.92
����Ԥ��2017���ҹ���������������������Լ1.92�ڶ�
������������������ͼ������y��t֮����ڽ�ǿ������ع�ϵ������֪���ݴ������ϵ�����̣��ɵô𰸣���������֪�е����ݣ�����ع�ϵ�����ɵûع鷽�̣�2017���Ӧ��tֵΪ10�������Ԥ��2017���ҹ���������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��.
��.
��1����![]() �ڵ�
�ڵ�![]() ����������ֱ��
����������ֱ��![]() ��ֱ����ʵ��
��ֱ����ʵ��![]() ��ֵ��
��ֵ��
��2������![]() �ĵ������䣻
�ĵ������䣻
��3�����ۺ���![]() ������
������![]() �����ĸ���.
�����ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c����cosC= ![]() ��
��
��1�����B�Ĵ�С��
��2����BDΪAC���ϵ����ߣ�cosA= ![]() ��BD=
��BD= ![]() �����ABC�������
�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x���Ƕ�����R�ϵ�ż��������x��0ʱ��f��x��=log ![]() ����x+1����
����x+1����
��1����f��x���Ľ���ʽ��
��2����f��a��1������1����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ���ҽ���
���ҽ���![]() ����Բ
����Բ![]() �����Ҷ���ֱ�Ϊ
�����Ҷ���ֱ�Ϊ![]() ������
������![]() ��ֱ��
��ֱ��![]() ����Բ����
����Բ����![]() ���㣬��
���㣬��![]() �������
�������![]() �������3����
�������3����
��������Բ![]() �ķ��̣�
�ķ��̣�
������![]() ��
��![]() �ᴹֱ��
�ᴹֱ��![]() ����Բ
����Բ![]() ��λ��ֱ��
��λ��ֱ��![]() ����Ķ��㣬������
����Ķ��㣬������![]() ������ֱ��
������ֱ��![]() ��б���Ƿ�Ϊ��ֵ����˵�����ɣ�
��б���Ƿ�Ϊ��ֵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ ![]() =1��a��b��0�������ҽ���F1��F2 �� ������Ϊ
=1��a��b��0�������ҽ���F1��F2 �� ������Ϊ ![]() ��˫���߷���Ϊ
��˫���߷���Ϊ ![]() =1��a��0��b��0����ֱ��x=2��˫���ߵĽ���ΪA��B����|AB|=
=1��a��0��b��0����ֱ��x=2��˫���ߵĽ���ΪA��B����|AB|= ![]() ��
��
��������Բ��˫���ߵķ��̣�
������F2��ֱ��l����Բ����M��N���㣬��˫������P��Q���㣬����F1MN��F1Ϊ��Բ���㣩������Բ�����ȡ���ֵʱ�����F1PQ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��= ![]() ��g��x��=
��g��x��= ![]() ��
��
��1����1��x��2ʱ����g��x����
��2����x��Rʱ����g��x���Ľ���ʽ����������ͼ�� 
��3����xf[g��x��]=2g[f��x��]�Ľ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC��x2+y2��2x+4y��4=0���Ƿ����б��Ϊ1��ֱ��l��ʹl��ԲC�صõ��ҳ�ABΪֱ����Բ��ԭ�㣬���������ֱ�ߵķ���l����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��= ![]() +
+ ![]() ��ͼ�����y��Գƣ���a��0��
��ͼ�����y��Գƣ���a��0��
��1����a��ֵ��
��2����f��x����[0��2]��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com