
【题目】在路边安装路灯,灯柱![]() 的高为
的高为![]() 米,路宽
米,路宽![]() 为23米,灯杆
为23米,灯杆![]() 与灯柱
与灯柱![]() 角,路灯采用锥形灯罩,灯罩轴线
角,路灯采用锥形灯罩,灯罩轴线![]() 与灯杆
与灯杆![]() 垂直,请你建立适当直角坐标系,解决以下问题:
垂直,请你建立适当直角坐标系,解决以下问题:
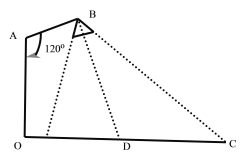
(1)当![]()
(2)![]() 且灯罩轴线
且灯罩轴线![]() 正好通过道路路面的中线时,求灯杆
正好通过道路路面的中线时,求灯杆![]() 的长为多少米?
的长为多少米?
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的的菱形,
的的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A,B,C的对边分别是a,b,c,且bcosB是acosC,ccosA的等差中项.
(1)求∠B的大小;
(2)若a+c= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2|x﹣a|.
(1)若函数y=f(x)为偶函数,求a的值;
(2)若a= ![]() ,求函数y=f(x)的单调递增区间;
,求函数y=f(x)的单调递增区间;
(3)当a>0时,若对任意的x∈(0,+∞),不等式f(x﹣1)≤2f(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S-ABC中,△ABC是边长为6的正三角形,SA=SB=SC=15,平面DEFH分别与AB,BC,SC,SA交于点D,E,F,H.且D,E分别是AB,BC的中点,如果直线SB∥平面DEFH,那么四边形DEFH的面积为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,a2=4,且对任意m,n,p,q∈N* , 若m+n=p+q,则有am+an=ap+aq . (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{ ![]() }的前n项和为Sn , 求证:
}的前n项和为Sn , 求证: ![]() ≤Sn<
≤Sn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),统计数据如表所示:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y | 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根据以上数据,绘制了散点图.

(1)根据散点图判断,在推广期内,![]() 与
与![]() (
(![]() ,
,![]() 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由);
的回归方程类型?(给出判断即可,不必说明理由);
(2)若y关于x的回归方程不是线性的可通过换元方法把它化归为线性回归方程。例如:![]() (a、b为常数,e为自然对数的底数),可以两边同时取自然对数
(a、b为常数,e为自然对数的底数),可以两边同时取自然对数![]() ,再令
,再令![]() ,先用最小二乘法求出
,先用最小二乘法求出![]() 与x的线性回归方程,再得出y与x的回归方程。根据(1)的判断结果及表1中的数据,求y关于x的回归方程;
与x的线性回归方程,再得出y与x的回归方程。根据(1)的判断结果及表1中的数据,求y关于x的回归方程;
(3)由(2)中的归方程预测活动推出第12天使用扫码支付的人次。
参考数据:
|
|
|
|
|
66 | 1.54 | 2711 | 50.12 | 3.47 |
其中![]() ,参考公式:对于一组数据
,参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:![]()
 ,
,![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com