
【题目】已知函数![]() .
.
(1)当a∈R时,讨论函数f(x)的单调性;
(2)对任意的x∈(1,+∞)均有f(x)<ax,若a∈Z,求a的最小值.
【答案】(1)答案不唯一,具体见解析(2)a的最小值为3
【解析】
(1)求得函数的导数![]() ,令
,令![]() ,分情况讨论
,分情况讨论![]() ,进而可得求得函数
,进而可得求得函数![]() 的单调性;
的单调性;
(2)由![]() 得到
得到![]() ,转化为
,转化为![]() ,对任意
,对任意![]() 成立,令
成立,令![]() ,利用导数求得函数
,利用导数求得函数![]() 的最大值,即可求得实数
的最大值,即可求得实数![]() 的最小值.
的最小值.
(1)由题意,函数![]() ,
,
则![]() ,x>0且x≠1,
,x>0且x≠1,
令![]() ,则其图象对称轴为直线x
,则其图象对称轴为直线x![]() ,g(0)=10,
,g(0)=10,
当![]() ,即a≥20时,则g(x)>0,f′(x)>0,
,即a≥20时,则g(x)>0,f′(x)>0,
此时f(x)分别在(0,1)和(1,+∞)上递增,
当![]() 时,即a<20时,令△=(a﹣20)2﹣400≤0.可得0≤a<20,
时,即a<20时,令△=(a﹣20)2﹣400≤0.可得0≤a<20,
所以当0≤a<20时,则g(x)>0,f′(x)>0,
此时f(x)分别在(0,1)和(1,+∞)上递增,
当a<0时,由g(x)=0解得x1![]() ,x2
,x2![]() ,
,
易知f(x)分别在(0,x1),(x2,+∞)上递增,分别在(x1,1),(1,x2)上递减.
综上所述,当a≥0时,f(x)分别在(0,1)和(1,+∞)上递增,
当a<0时,分别在(0,x1),(x2,+∞)上递增,分别在(x1,1),(1,x2)上递减.
(2)由题意得,![]() ,
,
即![]() ,对任意
,对任意![]() 成立,
成立,
令F(x)![]() ,x>1,则
,x>1,则![]() ,x>1,
,x>1,
令h(x)=(2﹣x)lnx+x﹣1,h′(x)=﹣lnx![]() ,x>1
,x>1
因为h′(x)在(1,+∞)上递减,且h′(1)=2>0,当x→+∞时,h′(x)→﹣∞,
所以存在x0∈(1,+∞),使得h′(x0)=0,且h(x)在(1,x0)上递增,在(x0,+∞)上递减,
因为h(1)=0,所以h(x0)>0,
因为当x→+∞时,h(x)→﹣∞,所以存在x1∈(x0,+∞),使得h(x1)=0,
且F(x)在(1,x1)上递增,在(x1,+∞)上递减,
所以F(x)max=F(x1)![]() ,
,
因为h(x1)=(2﹣x1)lnx1+x1﹣1=0,所以lnx1![]() ,所以F(x1)
,所以F(x1)![]() ,
,
因为h(4)=﹣2ln4+3=ln![]() 0,h(5)=﹣3ln5+4=ln
0,h(5)=﹣3ln5+4=ln![]() 0,所以x1∈[4,5],
0,所以x1∈[4,5],
令Φ(x)![]() ,x∈[4,5],易证Φ(x)在区间[4,5]上递减,
,x∈[4,5],易证Φ(x)在区间[4,5]上递减,
所以Φ(x)∈[![]() ,
,![]() ],
],
即F(x)max∈[![]() ,
,![]() ],因为a∈Z,所以a的最小值为3.
],因为a∈Z,所以a的最小值为3.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=2,AD=1.将矩形沿对角线BD折起,使A移到点P,P在平面BCD上的投影O恰好落在CD边上.
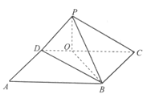
(1)证明:DP⊥平面BCP;
(2)求点O到平面PBD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某贫困村共有农户100户,均从事水果种植,平均每户年收入为1.8万元,在当地政府大力扶持和引导下,村委会决定2020年初抽出![]() 户(
户(![]() ,
,![]() )从事水果销售工作,经测算,剩下从事水果种植的农户平均每户年收入比上一年提高了
)从事水果销售工作,经测算,剩下从事水果种植的农户平均每户年收入比上一年提高了![]() ,而从事水果销售的农户平均每户年收入为
,而从事水果销售的农户平均每户年收入为![]() 万元.
万元.
(1)为了使从事水果种植的农户三年后平均每户年收入不低于2.4万元,那么2020年初至少应抽出多少农户从事水果销售工作?
(2)若一年后,该村平均每户的年收入为![]() (万元),问
(万元),问![]() 的最大值是否可以达到2.1万元?
的最大值是否可以达到2.1万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请解答以下问题,要求解决两个问题的方法不同.
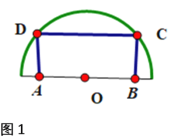
(1)如图1,要在一个半径为1米的半圆形铁板中截取一块面积最大的矩形![]() ,如何截取?并求出这个最大矩形的面积.
,如何截取?并求出这个最大矩形的面积.
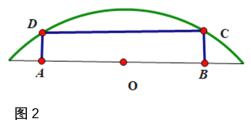
(2)如图2,要在一个长半轴为2米,短半轴为1米的半个椭圆铁板中截取一块面积最大的矩形![]() ,如何截取?并求出这个最大矩形的面积.
,如何截取?并求出这个最大矩形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 各项均为正数,
各项均为正数,![]() 为其前
为其前![]() 项的和,且
项的和,且![]() 成等差数列.
成等差数列.
(1)写出![]() 、
、![]() 、
、![]() 的值,并猜想数列
的值,并猜想数列![]() 的通项公式
的通项公式![]() ;
;
(2)证明(1)中的猜想;
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.若对于任意
项和.若对于任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com