练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，在正方体ABCDA1B1C1D1中，M，N分别是棱AB，CC1的中点，△MB1P的顶点P在棱CC1与棱C1D1上运动，有以下四个命题：

    ①平面MB1P⊥ND1；

    ②平面MB1P⊥平面ND1A1；

    ③△MB1P在底面ABCD上的射影图形的面积为定值；

    ④△MB1P在侧面DD1C1C上的射影图形是三角形．

    其中正确的命题序号是(　　)

    A. ①B. ②③

    C. ①③D. ②④

    【答案】B

    【解析】

    由正方体的几何性质及线面垂直、面面垂直等相关知识对四个命题进行判断

    ①平面,可用极限位置判断，当与重合时，平面不成立，故①错误；

    ②因为,且，平面，

    又平面，则平面平面，故②正确

    ③在底面上的射影图形的面积为定值，可以看到其投影三角形底边是，点在底面上的投影在上，故其到的距离不变，故投影图形的面积为定值，故③正确；

    ④当点落在点时，在侧面上的射影图形是条线段，故④错误，

    故正确的是②③，故选B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某中学每年暑假举行“学科思维讲座”活动，每场讲座结束时，所有听讲者都要填写一份问卷调查.2017年暑假某一天五场讲座收到的问卷分数情况如下表：

    用分层抽样的方法从这一天的所有问卷中抽取300份进行统计，结果如下表:

    （1）估计这次讲座活动的总体满意率；

    （2）求听数学讲座的甲某的调查问卷被选中的概率；

    （3）若想从调查问卷被选中且填写不满意的人中再随机选出5人进行家访，求这5人中选择的是理综讲座的人数的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位决定投资3200元建一仓库（长方体状），高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米长造价40元，两侧墙砌砖，每米长造价45元，顶部每平方米造价20元，求：

    （1）仓库顶部面积的最大允许值是多少？

    （2）为使达到最大，而实际投资又不超过预算，那么正面铁栅应设计为多长？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将正方形沿对角线折成直二面角，

    ①与平面所成角的大小为

    ②是等边三角形

    ③与所成的角为

    ④

    ⑤二面角为

    则上面结论正确的为_______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的几何体，底面ABFE是边长为2的正方形，DE与CF均垂直于平面ABFE，且．

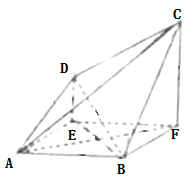
    （1）证明：BE∥平面ACD；

    （2）求三棱锥B﹣ACD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥PABCD中，侧面PAD是正三角形，底面ABCD是菱形，且∠ABC＝60°，M为PC的中点．

    (1)求证：PC⊥AD.

    (2)在棱PB上是否存在一点Q，使得A，Q，M，D四点共面？若存在，指出点Q的位置并证明；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校想了解高二数学成绩在学业水平考试中的情况，从中随机抽出人的数学成绩作为样本并进行统计，频率分布表如下表所示.

    组号

    分组

    频数

    频率

    第1组

    第2组

    第3组

    第4组

    第5组

    合计

    （1）据此估计这次参加数学考试的高二学生的数学平均成绩；

    （2）从这五组中抽取人进行座谈，若抽取的这人中，恰好有人成绩为分，人成绩为分，人成绩为分，人成绩为分，求这人数学成绩的方差；

    （3）从人的样本中，随机抽取测试成绩在内的两名学生，设其测试成绩分别为，.

    （i）求事件“”的概率；

    （ii）求事件“”的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中，，，点为棱的中点，点为线段上一动点.

    （Ⅰ）求证：当点为线段的中点时，平面；

    （Ⅱ）设，试问：是否存在实数，使得平面与平面所成锐二面角的余弦值为？若存在，求出这个实数；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，若曲线在点 处的切线方程为.

    （Ⅰ）求的解析式；

    （Ⅱ）求证：在曲线上任意一点处的切线与直线和所围成的三角形面积为定值，并求出此定值.

    查看答案和解析>>

    同步练习册答案