
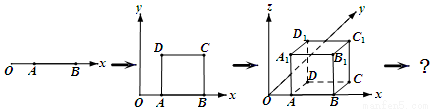
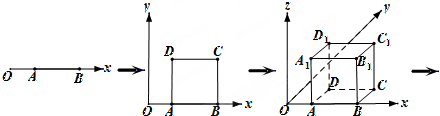
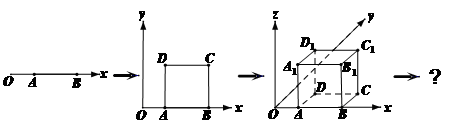
“点动成线,线动成面,面动成体”。如图,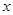 轴上有一条单位长度的线段
轴上有一条单位长度的线段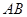 ,沿着与其垂直的
,沿着与其垂直的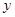 轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形
轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形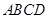 ),再把正方形沿着与其所在的平面垂直的
),再把正方形沿着与其所在的平面垂直的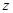 轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体
轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体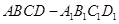 )。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有
)。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有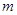 个顶点,
个顶点,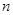 条棱,
条棱,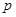 个面,则
个面,则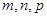 的值分别为
( )
的值分别为
( )
A.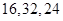 B.
B.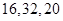 C.
C.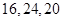 D.
D.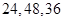
A
【解析】
试题分析:依题意,线段AB平移到CD位置后,可形成正方形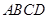 ,它有四个顶点、四条棱(边)、一个面;正方形
,它有四个顶点、四条棱(边)、一个面;正方形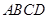 平移到正方形
平移到正方形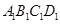 位置后,可形成正方体
位置后,可形成正方体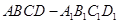 ,它有8个顶点、12条棱、6个面;
,它有8个顶点、12条棱、6个面;
把正方体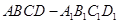 沿着与x轴、y轴、z轴都垂直的第四维方向进行平移得到四维方体后,
沿着与x轴、y轴、z轴都垂直的第四维方向进行平移得到四维方体后,
原来的8个顶点在平移后形成新的8个顶点,所以四维方体就共有8+8=16个顶点;
原先的8个顶点在平移的过程又形成新的8条棱,所以四维方体就共有12+12+8=32条棱;
正方体的12条棱在平移的过程都会形成一个新的面,所以四维方体就共有6+6+12=24个面;正方体的6个面在平移的过程中又各会形成一个正方体,所以四维方体中就包含有1+1+6=8个正方体.
考点:本小题主要考查类比推理.
点评:本题考查利用类比推理来说明空间中点线面之间的形成关系,解题的关键是理解点线面之间的:点动成线,线动成面,面动成体.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建厦门双十中学高三考前热身理数试卷 题型:填空题
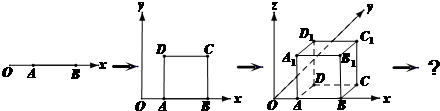
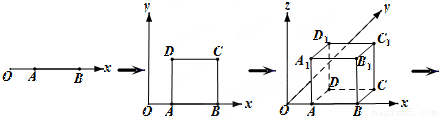
“点动成线,线动成面,面动成体”。如图,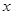 轴上有一条单位长度的线段
轴上有一条单位长度的线段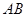 ,沿着与其垂直的
,沿着与其垂直的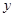 轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形
轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形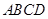 ),再把正方形沿着与其所在的平面垂直的
),再把正方形沿着与其所在的平面垂直的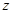 轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体
轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体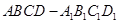 )。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有
)。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有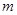 个顶点,
个顶点,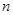 条棱,
条棱,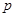 个面,则
个面,则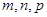 的值分别为
▲ .
的值分别为
▲ .
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省三明一中高二(下)第一次月考数学试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com