
【题目】已知圆M的方程为x2+y2-2x-2y-6=0,以坐标原点O为圆心的圆O与圆M相切.
(1)求圆O的方程;
(2)圆O与x轴交于E,F两点,圆O内的动点D使得DE,DO,DF成等比数列,求![]()
![]() 的取值范围.
的取值范围.
【答案】(1)x2+y2=2 (2)[![]() 1,0)
1,0)
【解析】
(1)化简圆M的方程为:x2+y2﹣2x﹣2y﹣6=0,为标准方程,求出圆心和半径,判定圆心O在圆M内部,因而内切,用|MN|=R﹣r,求圆O的方程;
(2)根据圆O与x轴交于E、F两点,圆内的动点D使得|DE|、|DO|、|DF|成等比数列,列出关系,再求![]()
![]() 的取值范围;
的取值范围;
(1)圆M的方程可整理为:(x![]() 1)2+(y-1)2=8,
1)2+(y-1)2=8,
故圆心M(1,1),半径R=2![]() .
.
圆O的圆心为O(0,0),
因为|MO|=![]() <2
<2![]() ,所以点O在圆M内,
,所以点O在圆M内,
故圆O只能内切于圆M.
设其半径为r.因为圆O内切于圆M,
所以有:|MO|=|R-r|,即![]() =|2
=|2![]()
![]() r|,解得r=
r|,解得r=![]() 或r=3
或r=3![]() (舍去);
(舍去);
所以圆O的方程为x2+y2=2.
(2)由题意可知:E(![]()
![]() ,0),F(
,0),F(![]() ,0).
,0).
设D(x,y),由|DE|、|DO|、|DF|成等比数列,
得|DO|2=|DE|×|DF|,
即:![]() ×
×![]() =x2+y2,
=x2+y2,
整理得:x2![]() y2=1.
y2=1.
![]()
![]() =(
=(![]()
![]() ,
,![]() y)(
y)(![]() ,
,![]() y)=x2+y2
y)=x2+y2![]() 2=2y2
2=2y2![]() 1,
1,
由于点D在圆N内,
故有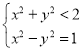 ,由此得y2<
,由此得y2<![]() ,
,
∴![]()
![]() 的取值范围是[
的取值范围是[![]() 1,0).
1,0).


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后人称之为三角形的欧拉线.已知△ABC的顶点A(2,0),B(0,4),且AC=BC,则△ABC的欧拉线的方程为( )
A.x+2y+3=0B.2x+y+3=0C.x﹣2y+3=0D.2x﹣y+3=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且对任意的实数
,且对任意的实数![]() 都有
都有![]() (
(![]() 是自然对数的底数),且
是自然对数的底数),且![]() ,若关于
,若关于![]() 的不等式
的不等式![]() 的解集中恰有两个负整数,则实数
的解集中恰有两个负整数,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数![]() 满足
满足![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 的最小值为0?若存在,求出
的最小值为0?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)若函数![]() ,是否存在实数
,是否存在实数![]() ,使函数
,使函数![]() 在
在![]() 上的值域为
上的值域为![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其最小正周期为
,其最小正周期为 ![]() .
.
(1)求 ![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后,再将得到的图象上各点的横坐标伸长到原来的
个单位长度后,再将得到的图象上各点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 ![]() 的图象,若关于
的图象,若关于 ![]() 的方程
的方程 ![]() 在区间
在区间 ![]() 上有解,求实数
上有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在P地正西方向8km的A处和正东方向1km的B处各有一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F,为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设![]()

![]() Ⅰ
Ⅰ![]() 为减少对周边区域的影响,试确定E,F的位置,使
为减少对周边区域的影响,试确定E,F的位置,使![]() 与
与![]() 的面积之和最小;
的面积之和最小;
![]() Ⅱ
Ⅱ![]() 为节省建设成本,求使
为节省建设成本,求使![]() 的值最小时AE和BF的值.
的值最小时AE和BF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com