
(1)求n;
(2)求含x2的项的系数;
(3)求展开式中所有的有理项.
解析:(1)通项公式为Tr+1=![]() .
.
∵第6项为常数项,
∴r=5时有![]() =0,即n=10.
=0,即n=10.
(2)令![]() =2,得r=
=2,得r=![]() (n-6)=2,
(n-6)=2,
∴所求的系数为![]() (-3)2=405.
(-3)2=405.
(3)根据通项公式,由题意得
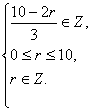 令
令![]() =k(k∈Z),
=k(k∈Z),
则10-2r=3k,即r=5-![]() k.
k.
∵r∈Z,∴k应为偶数.
∴k可取2,0,-2,即r可取2,5,8.
∴第3项,第6项与第9项为有理项,它们分别为![]() (-3)2x2,
(-3)2x2,![]() (-3)5,
(-3)5,![]() ·(-3)8x-2.
·(-3)8x-2.
小结:(1)本题是先求二项式的指数,再求与通项有关的其他问题.一般地,解此类问题可以分两步完成:第一步是根据所给出的条件(特定项)和通项公式,建立方程来确定指数〔求解时要注意二项式系数中n和r的隐含条件(n、r均为非负整数,n≥r)〕;第二步是根据所求的指数,再求所求解的项.此外,解本题时,为减少计算中的错误,宜把根式化为分数指数幂.
(2)题设展开式中有常数项的条件,实际上隐含了未知数的零次项的存在,所以n-2r=0,因此,由有常数项的条件可求得n.反之,若已知n,求展开式中常数项时,可先假设展开式的第r+1项为常数项,合并通项公式中同一字母的指数得f(r),然后令f(r)=0,从中求得r的非负整数值,即得所求的项.
(3)所谓求二项展开式中的有理项,一般是根据通项公式所得到的项,其所有的未知数的指数恰好都是整数的项.解这类型的问题必须合并通项公式中同一字母的指数,根据具体要求,令其属于整数,再根据数的整除性来求解.若求二项展开式中的整式项,则其通项公式中同一字母的指数应是非负整数.求解方式与求有理项一致.
(4)由本题的第(2)题知,二项式系数与系数是两个不同的概念,本题中x2项的系数为405,而x2项的二项式系数为![]() =45,初学者要能区别,切不可混淆.
=45,初学者要能区别,切不可混淆.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
| 3 | x |
| 1 | |||
2
|
| 3 | x |
| 1 | |||
2
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | x |
查看答案和解析>>
科目:高中数学 来源:黄冈中学 高二数学(下册)、考试卷1 排列、组合和二项式定理同步 题型:013
已知在二项式![]() 的展开式中第7项的系数最大,则n的值可以是
的展开式中第7项的系数最大,则n的值可以是
A.12
B.11,12
C.12,13
D.11,12,13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com