
【题目】在边长为8正方形![]() 中,点
中,点![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 上一点,且
上一点,且![]() ,若对于常数
,若对于常数![]() ,在正方形
,在正方形![]() 的边上恰有
的边上恰有![]() 个不同的点
个不同的点![]() ,使得
,使得![]() ,则实数
,则实数![]() 的取值范围为______.
的取值范围为______.
【答案】![]()
【解析】
建立平面直角坐标系,按照点P在线段![]() ,
,![]() ,
,![]() ,
,![]() 上进行逐段分析
上进行逐段分析![]() 的取值范围及对应的解,然后取各个范围的交集即可得答案.
的取值范围及对应的解,然后取各个范围的交集即可得答案.
以AB所在直线为x轴,以AD所在直线为y轴建立平面直角坐标系,如图所示,
则![]() ,
,![]() ,
,
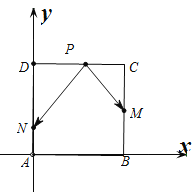
(1)当点P在AB上时,设![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∴当![]() 时有一解,当
时有一解,当![]() 时有两解;
时有两解;
(2)当点P在AD上时,设![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴当![]() 或
或![]() 时有一解,当
时有一解,当![]() 时有两解;
时有两解;
(3)若P在DC上,设![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∴当![]() 时有一解,当
时有一解,当![]() 时有两解;
时有两解;
(4)当点P在BC上时,设![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴当![]() 或
或![]() 时有一解,当
时有一解,当![]() 时有两解,
时有两解,
综上,在正方形![]() 的四条边上有且只有6个不同的点P,使得
的四条边上有且只有6个不同的点P,使得![]() 成立,那么m的取值范围是
成立,那么m的取值范围是![]() ,
,
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为![]() 的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
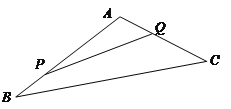
(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,造价均为每平方米100元.若围围墙用了20000元,问如何围可使竹篱笆用料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与圆
与圆![]() :
: ![]() 相切,且与圆
相切,且与圆![]() :
: ![]() 相内切,记圆心
相内切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .设
.设![]() 为曲线
为曲线![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交曲线
的平行线交曲线![]() 于
于![]() ,
, ![]() 两个不同的点.
两个不同的点.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)试探究![]() 和
和![]() 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(Ⅲ)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至2019年10月27日在中国武汉举行,第七届世界军人运动会是我国第一次承办的综合性国际军事体育赛事,也是继北京奥运会后我国举办的规模最大的国际体育盛会.经过激烈角逐,奖牌榜的前6名依次为中国俄罗斯巴西法国波兰和德国.其中德国队共有45名运动员获得了奖牌,其中金牌10枚银牌15枚铜牌20枚,某大学德语系同学利用分层抽样的方式从德国队获奖选手中抽取9名获奖代表.
(1)请问这9名获奖代表中获金牌银牌铜牌的人数分别为多少人?
(2)从这9人中随机抽取3人,记这3人中银牌选手的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面四边形
,底面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点.
上一点.
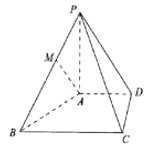
(1)若![]() ,则在线段
,则在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定
?若存在,请确定![]() 点的位置;若不存在,请说明理由
点的位置;若不存在,请说明理由
(2)己知![]() ,若异面直线
,若异面直线![]() 与
与![]() 成
成![]() 角,二而角
角,二而角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com