
| A. | (-∞,-1)∪(0,+∞) | B. | (-∞,0)∪(1,+∞) | C. | (-∞,0) | D. | (0,1) |
分析 由g(x)=f(x)-b有两个零点可得f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,则函数在定义域内不能是单调函数,结合函数图象可求a的范围
解答 解:∵g(x)=f(x)-b有两个零点,
∴f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,
由x3=x2可得,x=0或x=1
①当a>1时,函数f(x)的图象如图所示,此时存在b,满足题意,故a>1满足题意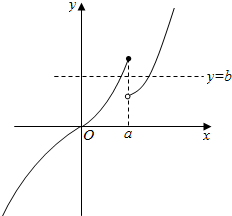
②当a=1时,由于函数f(x)在定义域R上单调递增,故不符合题意
③当0<a<1时,函数f(x)单调递增,故不符合题意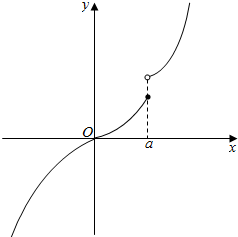
④a=0时,f(x)单调递增,故不符合题意
⑤当a<0时,函数y=f(x)的图象如图所示,此时存在b使得,y=f(x)与y=b有两个交点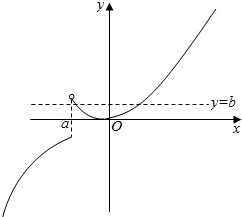
综上可得,a<0或a>1
则a的取值范围是(-∞,0)∪(1,+∞),
故选:B.
点评 本题考察了函数的零点问题,渗透了转化思想,数形结合、分类讨论的数学思想.


科目:高中数学 来源: 题型:选择题
 宜宾三中举行的电脑知识竞赛中,将高二年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、三、四、五小组的频率分别是0.30,0.15,0.10,0.05.则第二小组的小长方形的高为( )
宜宾三中举行的电脑知识竞赛中,将高二年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、三、四、五小组的频率分别是0.30,0.15,0.10,0.05.则第二小组的小长方形的高为( )| A. | 0.04 | B. | 0.40 | C. | 0.10 | D. | 0.025 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com