Question

若二次函数y=-x²+2x的定义域为[0，3]，则此二次函数的值域为（ ）
A．（-∞，1]
B．[-3，0]
C．[-3，1]
D．[3，+∞）

Answer 1

【答案】分析：先根据二次的对称轴及开口方向画出二次函数f（x）=x²-x+1的简图，结合图象，观察函数在给定区间上的单调性及最值点即可求得原函数的值域．
解答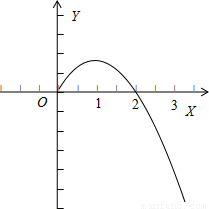：解：因为函数f（x）=-x²+2x的对称轴是：x=1，且开口向下，如图，
∴函数f（x）=-x²+2x在定义域[0，3]上的最大值为：y_x=1=-1²+2=1，
最小值为：y_x=3=-3²+2×3=-3，
∴函数f（x）=-x²+2x在定义域[0，3]上的值域为[-3，1]．
故答案为：C
点评：本题考查二次函数的值域，属于求二次函数的最值问题，考查运算求解能力，考查数形结合思想，属于基本题．