
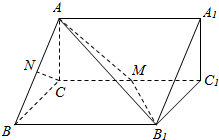
 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1的中点.分析 (1)通过证明BC⊥C1C,BC⊥AC,推出BC⊥平面ACC1A1,然后证明BC⊥AM.
(2)取AB1的中点P,连接MP,NP,证明NP∥B B1,推出NP∥CM,然后证明CN∥平面AB1M.
解答 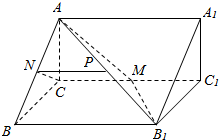 (1)证明:∵ABC-A1B1C1为直三棱柱,
(1)证明:∵ABC-A1B1C1为直三棱柱,
∴C1C⊥平面ABC,∴BC⊥C1C,
又BC⊥AC,∴BC⊥平面ACC1A1,
∵AM在平面ACC1A1上,∴BC⊥AM. …(6分)
(2)证明:取AB1的中点P,连接MP,NP,
∵P为A B1中点,N为AB中点,∴NP为△AB B1的中位线,∴NP∥B B1,
又∵C1C,B1B都是直三棱柱的棱,∴C1C∥B1B,M是棱CC1的中点,∴MC∥B1B,
∴NP∥CM,NP=$\frac{1}{2}$BB1=$\frac{1}{2}$CC1=CM,
∴NP$\underset{∥}{=}$CM,四边形CNPM为平行四边形,
∴NC∥PM,∴CN∥平面AB1M…(14分)
点评 本题考查直线与平面垂直的性质定理的应用,直线与平面平行的判定定理的应用,考查空间想象能力以及逻辑推理能力.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
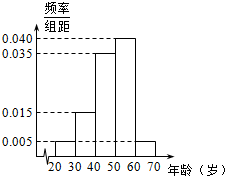 跳广场舞是现在广大市民喜爱的户外健身运动,某健身运动公司为了解本地区市民对跳广场舞的热衷程度,随机抽取了100名跳广场舞的市民,统计其年龄(单位:岁)并整理得到如下的频率分布直方图(其中年龄的分组区间分别为[20,30),[30,40),[40,50),[50,60),[60,70]),其中女性市民有55名,将所抽样本中年龄不小于50岁跳广场舞的市民称为“广舞迷”.已知其中有30名女性广舞迷.
跳广场舞是现在广大市民喜爱的户外健身运动,某健身运动公司为了解本地区市民对跳广场舞的热衷程度,随机抽取了100名跳广场舞的市民,统计其年龄(单位:岁)并整理得到如下的频率分布直方图(其中年龄的分组区间分别为[20,30),[30,40),[40,50),[50,60),[60,70]),其中女性市民有55名,将所抽样本中年龄不小于50岁跳广场舞的市民称为“广舞迷”.已知其中有30名女性广舞迷.| 广舞迷 | 非广舞迷 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com