
【题目】已知圆![]() ,
,![]() 是
是![]() 轴上的动点,
轴上的动点,![]() ,
,![]() 分别切圆
分别切圆![]() 于
于![]() ,
,![]() 两点.
两点.
(![]() )当
)当![]() 的坐标为
的坐标为![]() 时,求切线
时,求切线![]() ,
,![]() 的方程.
的方程.
(![]() )求四边形
)求四边形![]() 面积的最小值.
面积的最小值.
(![]() )若
)若![]() ,求直线
,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】将三颗骰子各掷一次,记事件A=“三个点数都不同”,B=“至少出现一个6点”,则条件概率P(A|B),P(B|A)分别是( )
A.![]() ,
, ![]()
B.![]() ,
, ![]()
C.![]() ,
, ![]()
D.![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线y2=4x的准线与x轴交于A点,焦点是F,P是位于x轴上方的抛物线上的任意一点,令m= ![]() ,当m取得最小值时,PA的斜率是( )
,当m取得最小值时,PA的斜率是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
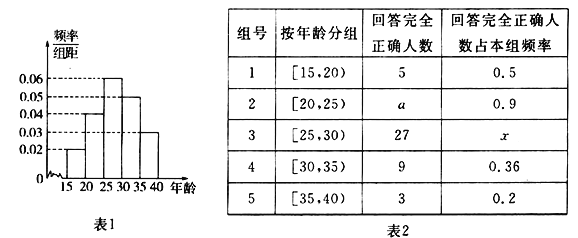
【题目】为办好省运会,计划招募各类志愿者1.2万人.为做好宣传工作,招募小组对15-40岁的人群随机抽取了100人,回答“省运会”的有关知识,根据统计结果制作了如下的统计图表1、表2:
(I)分别求出表2中的a、x的值;
(II)若在第2、3、4组回答完全正确的人中,用分层抽样的方法抽取6人,则各组应分别抽取多少人?
(III)在(II)的前提下,招募小组决定在所抽取的6人中,随机抽取2人颁发幸运奖,求获奖的2人均来自第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
(1)若对任意![]() ,且
,且![]() ,都有
,都有![]() ,则
,则![]() 为R上的减函数;
为R上的减函数;
(2)若![]() 为R上的偶函数,且在
为R上的偶函数,且在![]() 内是减函数,
内是减函数, ![]() (-2)=0,则
(-2)=0,则![]() >0解集为(-2,2);
>0解集为(-2,2);
(3)若![]() 为R上的奇函数,则
为R上的奇函数,则![]() 也是R上的奇函数;
也是R上的奇函数;
(4)t为常数,若对任意的![]() ,都有
,都有![]() 则
则![]() 关于
关于![]() 对称。
对称。
其中所有正确的结论序号为_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且x≤0时, f(x)=-x+1
(1)求f(0),f(2);
(2)求函数f(x)的解析式;
(3)若f(a-1)<3,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=ex+ax2 , g(x)是f(x)的导函数,
(1)当a>0时,求证:存在唯一的x0∈(﹣ ![]() ,0),使得g(x0)=0;
,0),使得g(x0)=0;
(2)若存在实数a,b,使得f(x)≥b恒成立,求a﹣b的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com