【题目】某村投资128万元建起了一处生态采摘园，预计在经营过程中，第一年支出10万元，以后每年支出都比上一年增加4万元，从第一年起每年的销售收入都为76万元．设y表示前n（n∈N*）年的纯利润总和（利润总和=经营总收入﹣经营总支出﹣投资）．
（1）该生态园从第几年开始盈利？
（2）该生态园前几年的年平均利润最大，最大利润是多少？
【答案】
（1）解：依题意，每年支出组成首项为10，公差为4的等差数列，可得前n年的总支出10n+ 
×4
可得前n（n∈N*）年的纯利润总和y=76n﹣[10n+ ×4]﹣128=﹣2n2+68n﹣128
由y＞0，即﹣2n2+68n﹣128＞0
解得2＜n＜32
由于n∈N+，故从第三年开始赢利
（2）解：年平均纯利润 
=﹣2n+68﹣ 
=68﹣2（n+ 
）≤36
当且仅当n=8时等号成立，此时年平均纯利润最大值为36万元，
即生态园前8年的年平均利润最大，最大利润是36万元
【解析】（1）每年的支出构成一个等差数列，每年的收入是一个常数列，故根据f利润总和=经营总收入﹣经营总支出﹣投资，可建立函数关系；（2）求出年平均纯利润，再利用基本不等式，即可求得年平均纯利润的最大值．
科目：高中数学 来源： 题型：
【题目】已知曲线方程C：x2+y2﹣2x﹣4y+m=0．
（1）当m=﹣6时，求圆心和半径；
（2）若曲线C表示的圆与直线l：x+2y﹣4=0相交于M，N，且 
，求m的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）=ax2+（b﹣2）x+3（a≠0）
（1）若不等式f（x）＞0的解集（﹣1，3）．求a，b的值；
（2）若f（1）=2，a＞0，b＞0求 
+ 
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，矩形草坪AMPN中，点C在对角线MN上．CD垂直于AN于点D，CB垂直于AM于点B，|CD|=|AB|=3米，|AD|=|BC|=2米，设|DN|=x米，|BM|=y米．求这块矩形草坪AMPN面积的最小值．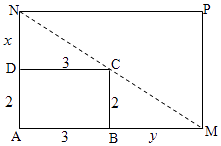 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点，且PA=AD．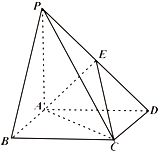 
（1）求证：PB∥平面AEC；
（2）求证：AE⊥平面PCD；
（3）设二面角D﹣AE﹣C为60°，且AP=1，求D到平面AEC的距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
（p﹣2）x2+（2q﹣8）x+1（p＞2，q＞0）．
（1）当p=q=3时，求使f（x）≥1的x的取值范围；
（2）若f（x）在区间[ ，2]上单调递减，求pq的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知实数p：x2﹣4x﹣12≤0，q：（x﹣m）（x﹣m﹣1）≤0
（1）若m=2，那么p是q的什么条件；
（2）若q是p的充分不必要条件，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设椭圆 
的离心率 
，椭圆上一点A到椭圆C两焦点的距离之和为4．
（1）求椭圆C的方程；
（2）直线l与椭圆交于A，B两点，且AB中点为 
，求直线l方程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
