
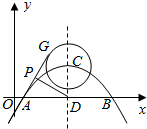
 已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )
已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )| A. | $\frac{7}{2}$ | B. | $\frac{{\sqrt{41}}}{2}$ | C. | $\frac{{\sqrt{34}}}{2}$ | D. | $2\sqrt{3}$ |
分析 求出抛物线的顶点坐标,写出圆的方程,设出G的坐标,推出P的坐标,利用两点间距离公式求解最值.
解答 解:抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,
可得A(1,0),B(9,0),D(5,0),C(5,3),圆的方程为:(x-5)2+(y-3)2=4,
设G(5+2cosθ,3+2sinθ).P为AG的中点,
可得P(3+cosθ,$\frac{3}{2}$+sinθ).
DP=$\sqrt{({cosθ-2)}^{2}+(\frac{3}{2}+sinθ)^{2}}$=$\sqrt{5+\frac{9}{4}-4cosθ+3sinθ}$=$\sqrt{5+\frac{9}{4}+5sin(θ-γ)}$,其中tanγ=$\frac{4}{3}$.
$\sqrt{5+\frac{9}{4}+5sin(θ-γ)}$≤$\sqrt{10+\frac{9}{4}}$=$\frac{7}{2}$.
故选:A.
点评 本题考查抛物线的简单性质以及圆的参数方程与三角函数的最值的求法,考查分析问题解决问题以及转化思想的应用.


科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | ( 1,6) | C. | (2,4) | D. | (2,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com