
【题目】函数f(x)= ![]() 的定义域为 .
的定义域为 .
【答案】[e2 , +∞)∪{1}
【解析】解:设g(x)=x﹣lnx﹣1,导数g′(x)= ![]() . 令g′(x)>0,得x>1,g(x)递增;令g′(x)<0,得0<x<1,g(x)递减.
. 令g′(x)>0,得x>1,g(x)递增;令g′(x)<0,得0<x<1,g(x)递减.
则g(x)的最小值为g(1)=0,即x﹣lnx﹣1≥0.
当x=1时,f(1)=0;
当x>0,且x≠1时,lnx﹣2≥0,解得x≥e2 .
则f(x)的定义域为:[e2 , +∞)∪{1}.
所以答案是:[e2 , +∞)∪{1}.
【考点精析】解答此题的关键在于理解函数的定义域及其求法的相关知识,掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.


科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
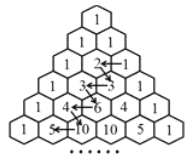
【题目】杨辉三角,是二项式系数在三角形中的一种几何排列。在欧洲,这个表叫做帕斯卡三角形。帕斯卡(1623——1662)是在1654年发现这一规律的,比杨辉要迟![]() 年,比贾宪迟
年,比贾宪迟![]() 年。如图的表在我国南宋数学家杨辉1261年所著的《详解九章算法》一书里就出现了,这又是我国数学史上的一个伟大成就。如图所示,在“杨辉三角”中,从1开始箭头所指的数组成一个锯齿形数列:
年。如图的表在我国南宋数学家杨辉1261年所著的《详解九章算法》一书里就出现了,这又是我国数学史上的一个伟大成就。如图所示,在“杨辉三角”中,从1开始箭头所指的数组成一个锯齿形数列:![]() ,则此数列前
,则此数列前![]() 项和为________.
项和为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子产品公司前四年的年宣传费x(单位:千万元)与年销售量y(单位:百万部)的数据如下表所示:
x(单位:千万元) | 1 | 2 | 3 | 4 |
y(单位:百万部) | 3 | 5 | 6 | 9 |
可以求y关于x的线性回归方程为 ![]() =1.9x+1.
=1.9x+1.
参考公式:回归方程 ![]() =
= ![]() x+
x+ ![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
(1)该公司下一年准备投入10千万元的宣传费,根据所求得的回归方程预测下一年的销售量m:
(2)根据下表所示五个散点数据,求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() .
.
x(单位:千万元) | 1 | 2 | 3 | 4 | 10 |
y(单位:百万部) | 3 | 5 | 6 | 9 | m |
并利用小二乘法的原理说明 ![]() =
= ![]() x+
x+ ![]() 与
与 ![]() =1.9x+1的关系.
=1.9x+1的关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知曲线C1的参数方程为 ![]() ,(α为参数,且α∈[0,π]),曲线C2的极坐标方程为ρ=﹣2sinθ.
,(α为参数,且α∈[0,π]),曲线C2的极坐标方程为ρ=﹣2sinθ.
(Ⅰ)求C1的极坐标方程与C2的直角坐标方程;
(Ⅱ)若P是C1上任意一点,过点P的直线l交C2于点M,N,求|PM||PN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=e2x﹣x2﹣a.
(1)证明f(x)在(﹣∞,+∞)上为增函数;
(2)当a=1时,解不等式f[f(x)]>x;
(3)若f[f(x)﹣x2﹣2x]>f(x)在(0,+∞)上恒成立,求a的最大整数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
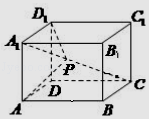
【题目】如图,在长方体ABCD﹣A1B1C1D1中, ![]() ,点P为线段A1C上的动点(包含线段端点),则下列结论正确的 . ①当
,点P为线段A1C上的动点(包含线段端点),则下列结论正确的 . ①当 ![]() 时,D1P∥平面BDC1;
时,D1P∥平面BDC1;
②当 ![]() 时,A1C⊥平面D1AP;
时,A1C⊥平面D1AP;
③当∠APD1的最大值为90°;
④AP+PD1的最小值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆. 
(1)若围墙AP、AQ总长度为200米,如何可使得三角形地块APQ面积最大?
(2)已知竹篱笆长为 ![]() 米,AP段围墙高1米,AQ段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
米,AP段围墙高1米,AQ段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D
的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D ![]() 在椭圆C上,直线l:y=kx+m与椭圆C相交于A、P两点,与x轴、y轴分别相交于点N和M,且PM=MN,点Q是点P关于x轴的对称点,QM的延长线交椭圆于点B,过点A、B分别作x轴的垂涎,垂足分别为A1、B1
在椭圆C上,直线l:y=kx+m与椭圆C相交于A、P两点,与x轴、y轴分别相交于点N和M,且PM=MN,点Q是点P关于x轴的对称点,QM的延长线交椭圆于点B,过点A、B分别作x轴的垂涎,垂足分别为A1、B1
(1)求椭圆C的方程;
(2)是否存在直线l,使得点N平分线段A1B1?若存在,求求出直线l的方程,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com