
【题目】如图,在四边形ABCD中,∠ABC= ![]() ,AB:BC=2:3,
,AB:BC=2:3, ![]() .
. 
(1)求sin∠ACB的值;
(2)若 ![]() ,CD=1,求△ACD的面积.
,CD=1,求△ACD的面积.
【答案】
(1)解:∵∠ABC= ![]() ,AB:BC=2:3,
,AB:BC=2:3, ![]() ,可得:AB=
,可得:AB= ![]() ,
,
∴在△ABC中,由余弦定理AC2=AB2+BC2﹣2ABBCcos∠ABC,可得:7= ![]() +BC2﹣
+BC2﹣ ![]() ,
,
∴解得:BC=3,AB=2,
∴由正弦定理可得:sin∠ACB= ![]() =
= ![]() =
= ![]()
(2)解:∵由(1)及余弦定理可得:
cos∠ACB= ![]() =
= ![]() =
= ![]() ,
,
∴sin ![]() =
= ![]() (cos∠ACB+sin∠ACB)
(cos∠ACB+sin∠ACB)
= ![]() (
( ![]() +
+ ![]() ),
),
∴S△ACD= ![]() ACCDsin∠ACD=
ACCDsin∠ACD= ![]() 1×
1× ![]() ×(
×( ![]() +
+ ![]() )=
)= ![]() .
.
【解析】(1)在△ABC中,由已知及余弦定理,比例的性质即可解得BC=3,AB=2,由正弦定理即可解得sin∠ACB的值(2)由(1)及余弦定理可求cos∠ACB,利用两角差的正弦函数公式可求sin∠ACD的值,利用三角形面积公式即可计算得解.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() ,以及对余弦定理的定义的理解,了解余弦定理:
,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】甲厂以x千克/小时的速度匀速生产某种产品(生产条件要求1≤x≤10),每小时可获得的利润是100(5x+1﹣ ![]() )元.
)元.
(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在ABC中,角A,B,C的对边分别为a,b,c,若△ABC为锐角三角形,且满足sinB(1+2cosC)=2sinAcosC+cosAsinC,则下列等式成立的是( )
A.a=2b
B.b=2a
C.A=2B
D.B=2A
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH
(3)求异面直线MN与AG所成角的余弦值

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ln(mx+1)﹣2(m≠0).
(1)讨论f(x)的单调性;
(2)若m>0,g(x)=f(x)+ ![]() 存在两个极值点x1 , x2 , 且g(x1)+g(x2)<0,求m的取值范围.
存在两个极值点x1 , x2 , 且g(x1)+g(x2)<0,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个分类变量x与y,其一组观测值如下面的2×2列联表所示:
y1 | y2 | |
x1 | a | 20-a |
x2 | 15-a | 30+a |
其中a,15-a均为大于5的整数,则a取何值时,在犯错误的概率不超过0.1的前提下认为x与y之间有关系?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市在海岛A上建了一水产养殖中心.在海岸线l上有相距70公里的B、C两个小镇,并且AB=30公里,AC=80公里,已知B镇在养殖中心工作的员工有3百人,C镇在养殖中心工作的员工有5百人.现欲在BC之间建一个码头D,运送来自两镇的员工到养殖中心工作,又知水路运输与陆路运输每百人每公里运输成本之比为1:2. 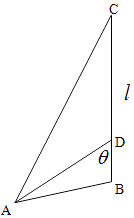
(1)求sin∠ABC的大小;
(2)设∠ADB=θ,试确定θ的大小,使得运输总成本最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1 , F2是椭圆 ![]() (0<b<2)的左、右焦点,过F1的直线l交椭圆于A,B两点,若|AF2|+|BF2|最大值为5,则椭圆的离心率为( )
(0<b<2)的左、右焦点,过F1的直线l交椭圆于A,B两点,若|AF2|+|BF2|最大值为5,则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系中椭圆C的方程为ρ2= ![]() ,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
(1)若椭圆上任一点坐标为P(x,y),求 ![]() 的取值范围;
的取值范围;
(2)若椭圆的两条弦AB,CD交于点Q,且直线AB与CD的倾斜角互补,求证:|QA||QB|=|QC||QD|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com