
【题目】如图,在![]() 中,点
中,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() ,
,![]() .
.
(1)求![]() ;
;
(2)若![]() 的面积是
的面积是![]() ,求
,求![]() .
.

【答案】(1)![]() (2)
(2)![]()
【解析】
(1)在![]() 中对角
中对角![]() 使用余弦定理求出
使用余弦定理求出![]() 的值,并判断出
的值,并判断出![]() 的形状,从而得出
的形状,从而得出![]() ;
;
(2)解法1:利用![]() 的面积求出
的面积求出![]() ,在该三角形中使用余弦定理求出
,在该三角形中使用余弦定理求出![]() ,利用正弦定理求出
,利用正弦定理求出![]() ,最后利用同角三角函数求出
,最后利用同角三角函数求出![]() ;
;
解法2:作![]() ,垂足为点
,垂足为点![]() ,结合
,结合![]() 的形状可求出
的形状可求出![]() ,由
,由![]() 的面积求出
的面积求出![]() ,并求出
,并求出![]() ,然后利用勾股定理求出
,然后利用勾股定理求出![]() ,然后在
,然后在![]() 中利用锐角三角函数求出
中利用锐角三角函数求出![]() 。
。
(1)在![]() 中,因为
中,因为![]() ,
,![]() ,
,![]()
由余弦定理得![]() ,
,
![]()
整理得![]() ,
,
解得![]() .
.
所以,![]() .
.
所以,![]() 是等边三角形,所以,
是等边三角形,所以,![]() .
.
(2)法1:因为![]() ,所以
,所以![]() .
.
因为![]() 的面积是
的面积是![]() ,
,
所以,![]() ,
,
所以,![]() .
.
在![]() 中,
中,
![]()
![]()
=![]()
所以![]() .
.
在![]() 中,由正弦定理得
中,由正弦定理得![]() ,
,
![]()
易知角![]() 为锐角,
为锐角,
![]()
法2:作![]() ,垂足为
,垂足为![]() ,
,
因为![]() 的等边三角形,
的等边三角形,
所以,![]()
因为![]() 的面积是
的面积是![]() ,
,
所以,![]() ,
,![]()
![]()
在![]() 中,
中,![]()
所以,在![]() 中,
中,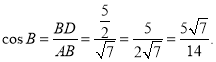


科目:高中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,BA=BC=![]() ,
,![]() ,在菱形BCDE中,
,在菱形BCDE中,![]() ,AE=
,AE=![]() .
.
(1)求证:平面ABC![]() 平面AEC;
平面AEC;
(2)设直线CE与平面ABE所成的角为![]() ,求
,求![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”,《中华人民共和国道路交通安全法》 第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼 让斑马线”行为统计数据:

(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口 9月份的不“礼让斑马线”违章驾驶员人数;
(3)若从表中3、4月份分别抽取4人和2人,然后再从中任选2 人进行交规调查,求抽到的两人恰好来自同一月份的概率.
参考公式: 
 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张军在网上经营了一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元/千克.为了增加销量,张军对以上四种干果进行促销,若一次性购买干果的总价达到150元,顾客就少付x(x∈Z)元,每笔订单顾客在网上支付成功后,张军会得到支付款的80%.
①当x=15时,顾客一次性购买松子和腰果各1千克,需要支付_________________元;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销的总价的70%,则x的最大值为___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值是
上的最大值是![]() ,最小值是
,最小值是![]() ,求
,求![]() 的值;
的值;
(2)用定义法证明![]() 在其定义域上是减函数;
在其定义域上是减函数;
(3)设![]() , 若对任意
, 若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且直线
,且直线![]() 恰好平分
恰好平分![]() .
.

(1)求![]() 的值;
的值;
(2)设![]() 是直线
是直线![]() 上一点,直线
上一点,直线![]() 交抛物线于另一点
交抛物线于另一点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月智能共享单车项目正式登陆某市,两种车型![]() “小绿车”、“小黄车”
“小绿车”、“小黄车”![]() 采用分时段计费的方式,“小绿车”每30分钟收费
采用分时段计费的方式,“小绿车”每30分钟收费![]() 元
元![]() 不足30分钟的部分按30分钟计算
不足30分钟的部分按30分钟计算![]() ;“小黄车”每30分钟收费1元
;“小黄车”每30分钟收费1元![]() 不足30分钟的部分按30分钟计算
不足30分钟的部分按30分钟计算![]() 有甲、乙、丙三人相互独立的到租车点租车骑行
有甲、乙、丙三人相互独立的到租车点租车骑行![]() 各租一车一次
各租一车一次![]() 设甲、乙、丙不超过30分钟还车的概率分别为
设甲、乙、丙不超过30分钟还车的概率分别为![]() ,
,![]() ,
,![]() ,三人租车时间都不会超过60分钟
,三人租车时间都不会超过60分钟![]() 甲、乙均租用“小绿车”,丙租用“小黄车”.
甲、乙均租用“小绿车”,丙租用“小黄车”.
![]() 求甲、乙两人所付的费用之和等于丙所付的费用的概率;
求甲、乙两人所付的费用之和等于丙所付的费用的概率;
![]() 2
2![]() 设甲、乙、丙三人所付的费用之和为随机变量
设甲、乙、丙三人所付的费用之和为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com