
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”,国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明![]() 如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形
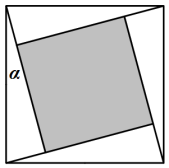
如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形![]() 若直角三角形中较小的锐角
若直角三角形中较小的锐角![]() ,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是
,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】“网购”已经成为我们日常生活中的一部分,某地区随机调查了100名男性和100名女性在“双十一”活动中用于网购的消费金额,数据整理如下:
男性消费金额频数分布表
消费金额 (单位:元) | 0~500 | 500~1000 | 1000~1500 | 1500~2000 | 2000~3000 |
人数 | 15 | 15 | 20 | 30 | 20 |
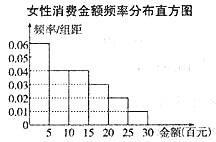
(1)试分别计算男性、女性在此活动中的平均消费金额;
(2)如果分别把男性、女性消费金额与中位数相差不超过200元的消费称作理性消费,试问是否有5成以上的把握认为理性消费与性别有关.
附: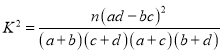
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() :
:![]() ,
,![]() :
:![]() .给出以下四个命题:
.给出以下四个命题:
①分别过点![]() ,
,![]() ,作
,作![]() 的不同于
的不同于![]() 轴的切线,两切线相交于点
轴的切线,两切线相交于点![]() ,则点
,则点![]() 的轨迹为椭圆的一部分;
的轨迹为椭圆的一部分;
②若![]() ,
,![]() 相切于点
相切于点![]() ,则点
,则点![]() 的轨迹恒在定圆上;
的轨迹恒在定圆上;
③若![]() ,
,![]() 相离,且
相离,且![]() ,则与
,则与![]() ,
,![]() 都外切的圆的圆心在定椭圆上;
都外切的圆的圆心在定椭圆上;
④若![]() ,
,![]() 相交,且
相交,且![]() ,则与
,则与![]() ,
,![]() 一个内切一个外切的圆的圆心的轨迹为椭圆的一部分.
一个内切一个外切的圆的圆心的轨迹为椭圆的一部分.
则以上命题正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过椭圆
过椭圆![]() 的右焦点,且交椭圆于A,B两点,线段AB的中点是
的右焦点,且交椭圆于A,B两点,线段AB的中点是![]() ,
,
(1)求椭圆的方程;
(2)过原点的直线l与线段AB相交(不含端点)且交椭圆于C,D两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率e满足
的离心率e满足![]() ,以坐标原点为圆心,椭圆C的长轴长为半径的圆与直线
,以坐标原点为圆心,椭圆C的长轴长为半径的圆与直线![]() 相切.
相切.
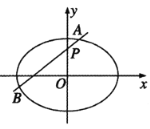
(1)求椭圆C的方程;
(2)过点P(0,1)的动直线![]() (直线
(直线![]() 的斜率存在)与椭圆C相交于A,B两点,问在y轴上是否存在与点P不同的定点Q,使得
的斜率存在)与椭圆C相交于A,B两点,问在y轴上是否存在与点P不同的定点Q,使得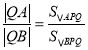 恒成立?若存在,求出定点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出定点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在创建“全国卫生文明城”的过程中,环保部门对某市市民进行了一次垃圾分类知识的网络问卷调查,每一位市民仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如下表所示.
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(Ⅰ)已知此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组中的数据用该组区间的中点值为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组中的数据用该组区间的中点值为代表),请利用正态分布的知识求![]() ;
;
(Ⅱ)在(Ⅰ)的条件下,环保部门为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ii)每次赠送的随机话费和相应的概率如下表.现市民甲要参加此次问卷调查,记![]() 为该市民参加问卷调查获赠的话费,求
为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
赠送的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1,在![]() 中,
中,![]() ,
,![]() ,E为
,E为![]() 中点.以
中点.以![]() 为折痕将
为折痕将![]() 折起,使点C到达点D的位置,且
折起,使点C到达点D的位置,且![]() 为直二面角,F是线段
为直二面角,F是线段![]() 上靠近A的三等分点,连结
上靠近A的三等分点,连结![]() ,
,![]() ,
,![]() ,如图2.
,如图2.
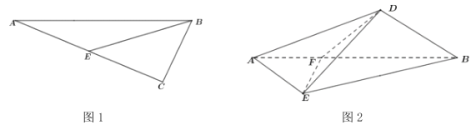
(1)证明:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】波罗尼斯(古希腊数学家,约公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数k(![]() 且
且![]() )的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.现有
)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.现有![]() ,
,![]() ,则当
,则当![]() 的面积最大时,AC边上的高为_______________.
的面积最大时,AC边上的高为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com