
| A. | ① | B. | ② | C. | ③ | D. | ④ |
分析 判断方程${{x}_{\;}}^{2}+2{x}_{\;}+3=0$的实根个数,可判断①;写出原命题的否定命题,可判断②;举出反例a=1,b=-1,可判断③; 根据互为逆否的两个命题真假性相同,可判断④.
解答 解:方程${{x}_{\;}}^{2}+2{x}_{\;}+3=0$的△=4-12<0,故方程无实根,
故①?x0∈R,使${x_0}^2+2{x_0}+3=0$为假命题;
②命题“?x0∈R,lgx0>0”的否定是“?x∈R,lgx≤0”,故②为假命题;
③如果a=1,b=-1∈R,则a>b,但a2=b2,故③为假命题;
④“若α=β,则sinα=sinβ”为真命题,故其逆否命题为真命题,故④为真命题.
故选:D
点评 本题以命题的真假判断与应用为载体,考查了特称命题,方程根的存在性及个数判断,不等式与不等关系,三角函数的定义等知识点,难度中档.


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
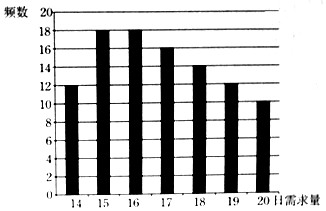 某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕成本为50元,每个蛋糕的售价为100元,如果当天卖不完,剩余的蛋糕作垃圾处理.现搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率.
某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕成本为50元,每个蛋糕的售价为100元,如果当天卖不完,剩余的蛋糕作垃圾处理.现搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
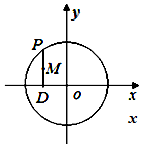 如图,在圆x2+y2=16上任取一点P,过点P作x 轴的垂线段PD,D为垂足,当点P在圆上运动时,则线段PD的中点M的轨迹方程为$\frac{x^2}{16}+\frac{y^2}{4}=1$.
如图,在圆x2+y2=16上任取一点P,过点P作x 轴的垂线段PD,D为垂足,当点P在圆上运动时,则线段PD的中点M的轨迹方程为$\frac{x^2}{16}+\frac{y^2}{4}=1$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
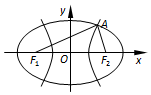 如图,F1,F2是椭圆C1与双曲线C2的公共焦点,点A是C1,C2的公共点.设C1,C2的离心率分别是e1,e2,∠F1AF2=2θ,则( )
如图,F1,F2是椭圆C1与双曲线C2的公共焦点,点A是C1,C2的公共点.设C1,C2的离心率分别是e1,e2,∠F1AF2=2θ,则( )| A. | ${e_1}^2{sin^2}θ+{e_2}^2{cos^2}θ=e_1^2e_2^2$ | |
| B. | ${e_2}^2{sin^2}θ+{e_1}^2{cos^2}θ=e_1^2e_2^2$ | |
| C. | ${e_2}^2{sin^2}θ+{e_1}^2{cos^2}θ=1$ | |
| D. | ${e_1}^2{sin^2}θ+{e_2}^2{cos^2}θ=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com