
分析 ①根据正弦定理进行证明
②根据三角函数的倍角公式以及正弦定理进行转化求解,
③作出如图的三角形AD⊥BC,可以得出$|\overrightarrow{AB}|$sinB=$|\overrightarrow{AC}|$sinC=AD,由此对已知条件变形即可得出结论
④设△ABC中的三边长为a,a+1,a+2最小角,最小角和最大角为θ,2θ,分别由正弦定理和余弦定理,求出cosθ,解得即可.
解答 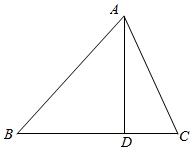 解:①由正弦定理得在三角形中A<B?a<b?sinA<sinB;故①正确,
解:①由正弦定理得在三角形中A<B?a<b?sinA<sinB;故①正确,
②若a,b,c为△ABC的三边且a=$\sqrt{3}$,B=2A,
则由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}=\frac{b}{sin2A}$=$\frac{b}{2sinAcosA}$,
即b=2acosA=2$\sqrt{3}$cosA,
∵C=π-A-B=π-3A>0,
∴0<A<$\frac{π}{3}$,即$\frac{1}{2}$<cosA<1,
则$\sqrt{3}$<2$\sqrt{3}$cosA<2$\sqrt{3}$,
则b的取值范围是($\sqrt{3},2\sqrt{3}$);故②正确,
③作出如图的图形AD⊥BC,由于$|\overrightarrow{AB}|$sinB=$|\overrightarrow{AC}|$sinC=AD,
∴$\overrightarrow{OP}=\overrightarrow{OA}+λ(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|sinB}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|sinC})$=$\overrightarrow{OA}+\frac{λ}{|AD|}(\overrightarrow{AB}+\overrightarrow{AC})$
由加法法则知,P在三角形的中线上
故动点P的轨迹一定通过△ABC的重心,故③错误,
④设△ABC中的三边长为a,a+1,a+2最小角,z∈N•,
最小角和最大角为θ,2θ,
再由正弦定理可得$\frac{a}{sinθ}$=$\frac{a+2}{sin2θ}$,
所以cosθ=$\frac{a+2}{2a}$,
由余弦定理得cosθ=$\frac{(a+2)^{2}+(a+1)^{2}-{a}^{2}}{2(a+2)(a+1)}$=$\frac{a+2}{2a}$,解得a=4,
所以三边的长为4,5,6.
则则cosθ=$\frac{a+2}{2a}$=$\frac{4+2}{2×4}=\frac{6}{8}$=$\frac{3}{4}$.
即最小角的余弦值为$\frac{3}{4}$.故④正确,
故答案为:①②④
点评 本题主要考查命题的真假判断,涉及三角函数的图象和性质,正弦定理以及平面向量的应用,涉及的综合性较强,有一定的难度.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (1,+∞) | C. | (0,1)∪(1,+∞) | D. | (-∞,0)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
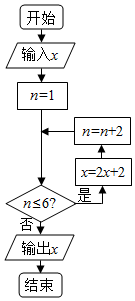
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{7}{30}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| Y X | y1 | y2 | 总计 |
| x1 | a | 10 | a+10 |
| x2 | c | 50 | c+50 |
| 总计 | 40 | 60 | 100 |
| A. | a=10,c=30 | B. | a=15,c=25 | C. | a=20,c=20 | D. | a=30,c=10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com