
【题目】如图①,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折起,使
折起,使![]() ,连接
,连接![]() 、
、![]() ,得到如图②所示的几何体.
,得到如图②所示的几何体.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在线段
在线段![]() 上,直线
上,直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】某初级中学共有学生2000名,各年级男生女生人数如表: 已知在全校学生中随机抽取1名,抽到的是初二年级女生的概率是0.19.
初一年级 | 初二年级 | 初三年级 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
(1)求x的值.
(2)现用分层抽样法在全校抽取48名学生,问应在初三年级学生中抽取多少名?
(3)已知y≥245,z≥245,求初三年级女生比男生多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信作为一款社交软件已经在支付,理财,交通,运动等各方面给人的生活带来各种各样的便利.手机微信中的“微信运动”,不仅可以看自己每天的运动步数,还可以看到朋友圈里好友的步数. ![]() 先生朋友圈里有大量好友使用了“微信运动”这项功能.他随机选取了其中40名,记录了他们某一天的走路步数,统计数据如下表所示:
先生朋友圈里有大量好友使用了“微信运动”这项功能.他随机选取了其中40名,记录了他们某一天的走路步数,统计数据如下表所示:

(1)以样本估计总体,视样本频率为概率,在![]() 先生的微信朋友圈里的男性好友中任意选取3名,其中走路步数不低于6000步的有
先生的微信朋友圈里的男性好友中任意选取3名,其中走路步数不低于6000步的有![]() 名,求
名,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)如果某人一天的走路步数不低于8000步,此人将被“微信运动”评定为“运动达人”,否则为“运动鸟人”.根据题意完成下面的![]() 列联表,并据此判断能否有90%以上的把握认为“评定类型”
列联表,并据此判断能否有90%以上的把握认为“评定类型”
与“性别”有关?

附:![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别是
)的左、右焦点分别是![]() ,
,![]() ,点
,点![]() 为
为![]() 的上顶点,点
的上顶点,点![]() 在
在![]() 上,
上,![]() ,且
,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,垂直于
两点,垂直于![]() 的直线
的直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图1).因其经济又环保,至今还在农业生产中得到使用(如图2).假定在水流量稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动.因筒车上盛水筒的运动具有周期性,可以考虑利用三角函数模型刻画盛水筒(视为质点)的运动规律.将筒车抽象为一个几何图形,建立直角坐标系(如图3).设经过t秒后,筒车上的某个盛水筒![]() 从点P0运动到点P.由筒车的工作原理可知,这个盛水筒距离水面的高度H(单位:
从点P0运动到点P.由筒车的工作原理可知,这个盛水筒距离水面的高度H(单位: ![]() ),由以下量所决定:筒车转轮的中心O到水面的距离h,筒车的半径r,筒车转动的角速度ω(单位:
),由以下量所决定:筒车转轮的中心O到水面的距离h,筒车的半径r,筒车转动的角速度ω(单位: ![]() ),盛水筒的初始位置P0以及所经过的时间t(单位:
),盛水筒的初始位置P0以及所经过的时间t(单位:![]() ).已知r=3
).已知r=3![]() ,h=2
,h=2![]() ,筒车每分钟转动(按逆时针方向)1.5圈, 点P0距离水面的高度为3.5
,筒车每分钟转动(按逆时针方向)1.5圈, 点P0距离水面的高度为3.5![]() ,若盛水筒M从点P0开始计算时间,则至少需要经过_______
,若盛水筒M从点P0开始计算时间,则至少需要经过_______![]() 就可到达最高点;若将点
就可到达最高点;若将点![]() 距离水面的高度
距离水面的高度![]() 表示为时间
表示为时间![]() 的函数,则此函数表达式为_________.
的函数,则此函数表达式为_________.



图1 图2 图3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将标号为1,2,…,20的20张卡片放入下列表格中,一个格放入一张卡片.把每列标号最小的卡片选出,将这些卡片中标号最大的数设为a;把每行标号最大的卡片选出,将这些卡片中标号最小的数设为b.
甲同学认为a有可能比b大,乙同学认为a和b有可能相等.那么甲乙两位同学中说法正确的同学是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某艺术团组织的“微视频展示”活动中,该团体将从微视频的“点赞量”和“专家评分”两个角度来进行评优.若A视频的“点赞量”和“专家评分”中至少有一项高于B视频,则称A视频不亚于B视频.已知共有5部微视频展,如果某微视频不亚于其他4部视频,就称此视频为优秀视频.那么在这5部微视频中,最多可能有_______个优秀视频.
查看答案和解析>>
科目:高中数学 来源: 题型:
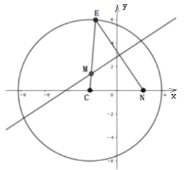
【题目】已知点![]() ,在圆
,在圆![]() :
:![]() 上任取一点
上任取一点![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .(如图).
.(如图).
(1)求点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)若过点![]() 的动直线
的动直线![]() 与(1)中的轨迹
与(1)中的轨迹![]() 相交于
相交于![]() 、
、![]() 两点.问:平面内是否存在异于点
两点.问:平面内是否存在异于点![]() 的定点
的定点![]() ,使得
,使得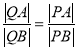 恒成立?试证明你的结论.
恒成立?试证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() .以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线
.以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线![]() ,从原点O作射线交
,从原点O作射线交![]() 于点M,点N为射线OM上的点,满足
于点M,点N为射线OM上的点,满足![]() ,记点N的轨迹为曲线C.
,记点N的轨迹为曲线C.
(Ⅰ)求出直线![]() 的参数方程和曲线C的直角坐标方程;
的参数方程和曲线C的直角坐标方程;
(Ⅱ)设直线![]() 与曲线C交于P,Q两点,求
与曲线C交于P,Q两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com