
【题目】空间中![]() 个平面,其中任意三个平面无公垂面.那么,下述四个结论
个平面,其中任意三个平面无公垂面.那么,下述四个结论
1没有任何两个平面互相平行;
2没有任何三个平面相交于一条直线;
3平面间的任意两条交线都不平行;
4平面间的每一条交线均与![]() 个平面相交.
个平面相交.
其中,正确的各数为( ).
A. 1 B. 2 C. 3 D. 4
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某班上午有五节课,分別安排语文,数学,英语,物理,化学各一节课.要求语文与化学相邻,数学与物理不相邻,且数学课不排第一节,则不同排课法的种数是
A. 24B. 16C. 8D. 12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-mlnx,h(x)=x2-x+a.
(1)当a=0时,f(x)≥h(x)在(1,+∞)上恒成立,求实数m的取值范围;
(2)当m=2时,若函数k(x)=f(x)-h(x)在区间(1,3)上恰有两个不同零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 件产品中,有
件产品中,有![]() 件正品,
件正品,![]() 件次品,从这
件次品,从这![]() 件产品中任意抽取
件产品中任意抽取![]() 件.
件.
(1)共有多少种不同的抽法?
(2)抽出的![]() 件中恰有
件中恰有![]() 件次品的抽法有多少种?
件次品的抽法有多少种?
(3)抽出的![]() 件中至少有
件中至少有![]() 件次品的抽法有多少种?
件次品的抽法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有三种股票,前两种的股数之和等于第三种的股数, 第二种股票的总价值是第一种股票的4 倍,第一、二种股票的总价值等于第三种股票的总价值,第二种股票每股比第一种股票贵![]() 元到2元,而第三种股票每股的价值不小于
元到2元,而第三种股票每股的价值不小于![]() 元而不大于6元.求在股票总量中第一种股票股数占总股数的百分比的最大值与最小值.
元而不大于6元.求在股票总量中第一种股票股数占总股数的百分比的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果在一条平面曲线上存在四点,使得这四点构成的图形是一个菱形,则称该曲线存在内接菱形.现已知双曲线![]() ,双曲线
,双曲线![]() ,其中
,其中![]() ,
,![]() ,
,![]() .证明:在双曲线
.证明:在双曲线![]() 与
与![]() 中有且仅有一条存在内接菱形.
中有且仅有一条存在内接菱形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某船由甲地逆水行驶到乙地,甲、乙两地相距s(km),水的流速为常量a(![]() ),船在静水中的最大速度为b(
),船在静水中的最大速度为b(![]() )(
)(![]() ),已知船每小时的燃料费用(以元为单位)与船在静水中的速度的平方成正比,比例系数为k,则船在静水中的航行速度为多少时,其全程的燃料费用最省?
),已知船每小时的燃料费用(以元为单位)与船在静水中的速度的平方成正比,比例系数为k,则船在静水中的航行速度为多少时,其全程的燃料费用最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,我国突发新冠肺炎疫情.面对“突发灾难”,举国上下心,继解放军医疗队于除夕夜飞抵武汉,各省医疗队也陆续增援,纷纷投身疫情防控与病人救治之中.为分担“逆行者”的后顾之忧,某大学学生志愿者团队开展“爱心辅学”活动,为抗疫前线工作者子女在线辅导功课.现随机安排甲、乙、丙3名志愿者为某学生辅导数学、物理、化学、生物4门学科,每名志愿者至少辅导1门学科,每门学科由1名志愿者辅导,则数学学科恰好由甲辅导的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
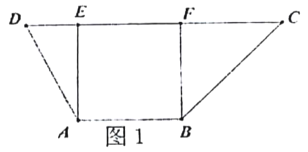
【题目】在梯形![]() 中(图1),
中(图1),![]() ,
, ![]() ,
, ![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() 、
、![]() ,已知
,已知![]() ,
, ![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,使得
同侧折起,使得![]() ,
, ![]() ,得空间几何体
,得空间几何体![]() (图2).
(图2).
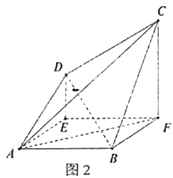
(1)证明: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com