
【题目】如图,在底面是正三角形的三棱锥![]() 中,D 为PC的中点,
中,D 为PC的中点,![]() ,
,![]()

(1)求证:![]() 平面
平面![]() ;
;
(2)求 BD 与平面 ABC 所成角的大小;
(3)求二面角![]() 的余弦值.
的余弦值.
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税法》第十四条中有下表(部分):
个人所得税税率(工资、薪金所得适用)
级数 | 全月应纳所得额 | 税率(%) |
1 | 不超过 |
|
2 | 超过 |
|
3 | 超过 |
|
4 | 超过 |
|
5 | 超过 |
|
上表中“全月应纳税所得额”是从月工资、薪金收入中减去![]() 元后的余额.如果某人月工资、薪金收入为
元后的余额.如果某人月工资、薪金收入为![]() 元,那么他应纳的个人所得税为________元.
元,那么他应纳的个人所得税为________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解我市参加2018年全国高中数学联赛的学生考试结果情况,从中选取60名同学将其成绩(百分制,均为正数)分成![]() 六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
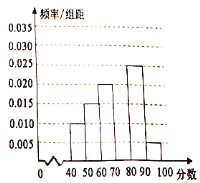
(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次考试成绩的众数、中位数、均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018广东深圳市高三一模】已知椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 与椭圆有且只有一个交点
与椭圆有且只有一个交点![]() .
.
(I)求椭圆![]() 的方程和点
的方程和点![]() 的坐标;
的坐标;
(II) ![]() 为坐标原点,与
为坐标原点,与![]() 平行的直线
平行的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
, ![]() ,求
,求![]() 的面积最大时直线
的面积最大时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为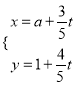 (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 的两个交点为
的两个交点为![]() ,
, ![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国![]() 标准采用世界卫生组织设定的最宽限值,即
标准采用世界卫生组织设定的最宽限值,即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某城市环保局从该市市区2017年上半年每天的
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某城市环保局从该市市区2017年上半年每天的![]() 监测数据中随机抽取18天的数据作为样本,将监测值绘制成茎叶图如下图所示(十位为茎,个位为叶).
监测数据中随机抽取18天的数据作为样本,将监测值绘制成茎叶图如下图所示(十位为茎,个位为叶).
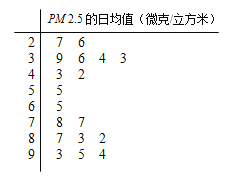
(Ⅰ)在这18个数据中随机抽取3个数据,求其中恰有2个数据为空气质量达到一级的概率;
(Ⅱ)在这18个数据中随机抽取3个数据,用![]() 表示其中不超标数据的个数,求
表示其中不超标数据的个数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)以这18天的![]() 日均值来估计一年的空气质量情况,则一年(按360天计算)中约有多少天的空气质量为二级.
日均值来估计一年的空气质量情况,则一年(按360天计算)中约有多少天的空气质量为二级.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足f(4)=f(﹣2)=1,f′(x)为f(x)的导函数,且导函数y=f′(x)的图象如图所示.则不等式f(x)<1的解集是( )
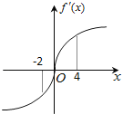
A. (﹣2,0)
B. (﹣2,4)
C. (0,4)
D. (﹣∞,﹣2)∪(4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
. ![]() 为椭圆的右焦点,
为椭圆的右焦点, ![]() 为椭圆上关于原点对称的两点,连接
为椭圆上关于原点对称的两点,连接![]() 分别交椭圆于
分别交椭圆于![]() 两点.
两点.
⑴求椭圆的标准方程;
⑵若![]() ,求
,求![]() 的值;
的值;
⑶设直线![]() ,
, ![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com