
【题目】已知圆![]() .
.
(1)求证:对任意实数![]() ,该圆恒过一定点;
,该圆恒过一定点;
(2)若该圆与圆![]() 外切,求
外切,求![]() 的值.
的值.
 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上上分别写着数字1,2,3,5,同时投掷这两枚玩具一次,记![]() 为两个朝下的面上的数字之和.
为两个朝下的面上的数字之和.
(1)求事件“![]() 不小于6”的概率;
不小于6”的概率;
(2)“![]() 为奇数”的概率和“
为奇数”的概率和“![]() 为偶数”的概率是不是相等?证明你作出的结论.
为偶数”的概率是不是相等?证明你作出的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个不透明的盒子中,放有标号分别为![]() ,
,![]() ,
,![]() ,
,![]() 的四个大小相同的小球,现从这个盒子中,有放回地先后取得两个小球,其标号分别为
的四个大小相同的小球,现从这个盒子中,有放回地先后取得两个小球,其标号分别为![]() ,
,![]() .
.
(1)求事件![]() 的概率;
的概率;
(2)求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌茶壶的原售价为80元一个,今有甲、乙两家茶具店销售这种茶壶,甲店用如下的方法促销:如果只购买一只茶壶,其价格为78元/个;如果一次购买两个茶壶,其价格为76元/个;…;如果一次购买的茶壶数每增加一个,那么茶壶的价格减少2元/个,但茶壶的售价不得低于44元/个。乙店一律按原价的75%销售。现某茶社要购买这种茶壶![]() 个,如果全部在甲店购买,则所需金额为
个,如果全部在甲店购买,则所需金额为![]() 元;如果全部在乙店购买,则所需金额为
元;如果全部在乙店购买,则所需金额为![]() 元。
元。
(1)分别求出![]() 、
、![]() 与
与![]() 之间的函数关系式。
之间的函数关系式。
(2)该茶社去哪家茶具店购买茶壶花费较少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1是四棱锥的直观图,其正(主)视图和侧(左)视图均为直角三角形,俯视图外框为矩形,相关数据如图2所示.
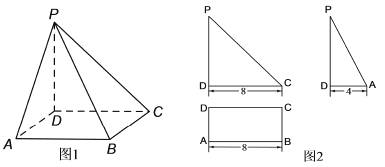
(1)设![]() 中点为
中点为![]() ,在直线
,在直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)若二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求四棱锥
,求四棱锥![]() 的外接球的表面积.
的外接球的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有![]() 、
、![]() 、
、![]() 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点![]() ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为![]()
![]() ,
,![]()
![]() ,
,![]()
![]() .假定
.假定![]() 、
、![]() 、
、![]() 、
、![]() 四点在同一平面内.
四点在同一平面内.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)求点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角三角形![]() 的顶点坐标
的顶点坐标![]() ,直角顶点
,直角顶点![]() ,顶点
,顶点![]() 在
在![]() 轴上,点
轴上,点![]() 为线段
为线段![]() 的中点,三角形
的中点,三角形![]() 外接圆的圆心为
外接圆的圆心为![]() .
.
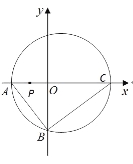
(1)求![]() 边所在直线方程;
边所在直线方程;
(2)求圆![]() 的方程;
的方程;
(3)直线![]() 过点
过点![]() 且倾斜角为
且倾斜角为![]() ,求该直线被圆
,求该直线被圆![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发![]() 个红包,每个红包金额为
个红包,每个红包金额为![]() 元,
元,![]() .已知在每轮游戏中所产生的
.已知在每轮游戏中所产生的![]() 个红包金额的频率分布直方图如图所示.
个红包金额的频率分布直方图如图所示.
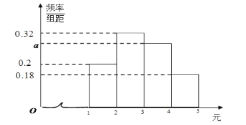
(1)求![]() 的值,并根据频率分布直方图,估计红包金额的众数;
的值,并根据频率分布直方图,估计红包金额的众数;
(2)以频率分布直方图中的频率作为概率,若甲、乙、丙三人从中各抢到一个红包,其中金额在![]() 的红包个数为
的红包个数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com