
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,若
,若![]() 且
且![]() 时,有
时,有![]() 成立.
成立.
(1)判断![]() 在
在![]() 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(2)解不等式![]() ;
;
(3)若![]() 对所有的
对所有的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)利用函数单调性的定义,奇函数的性质,结合![]() ,判断
,判断![]() 在
在![]() 上的单调递增;
上的单调递增;
(2) 根据(1)的结论,以及函数的定义域,列出不等式组,求出x的范围;
(3)根据(1)的结论和条件,将问题转化为m2-2am+1≥1,即m2-2am≥0对a∈[-1,1]恒成立,构造函数g(a)= -2ma+m2,进而求得m的取值范围.
任取x1,x2∈[-1,1]且x1<x2,则-x2∈[-1,1],
∵f(x)为奇函数,∴f(-x2)= -f(x2),
∴f(x1)-f(x2)=f(x1)+f(-x2)=![]()
由已知得![]() >0,
>0,![]() <0,
<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),∴f(x)在[-1,1]上单调递增.
(2)∵f(x)在[-1,1]上单调递增,∴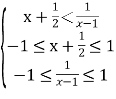 ,解得
,解得![]()
(3)∵f(1)=1,f(x)在[-1,1]上单调递增,∴在[-1,1]上,f(x)≤1.
问题转化为m2-2am+1≥1,即m2-2am≥0,对a∈[-1,1]恒成立.
设g(a)=-2m·a+m2.
①若m=0,则g(a)=0≥0,对a∈[-1,1]恒成立.
②若m≠0,则g(a)为a的一次函数,若g(a)≥0,对a∈[-1,1]恒成立,必须g(-1)≥0,且g(1)≥0,∴m≤-2或m≥2.
∴m的取值范围是m=0或m≤-2或m≥2.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】第一次大考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于![]() 分为优秀,
分为优秀,![]() 分以下为非优秀,统计成绩后,得到如下
分以下为非优秀,统计成绩后,得到如下![]() 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部![]() 人中随机抽取
人中随机抽取![]() 人为优秀的概率为
人为优秀的概率为![]() .
.
(I)请完成![]() 列联表:
列联表:
优秀 | 非优秀 | 合计 | |
甲班 |
| ||
乙班 |
| ||
合计 |
|
(Ⅱ)根据列联表的数据能否在犯错误的概率不超过![]() 的前提下认为成绩与班级有关系?
的前提下认为成绩与班级有关系?
参考公式和临界值表:
 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣2x﹣3≤0},B={x|x2﹣2mx+m2﹣4≤0,x∈R,m∈R}.
(1)若A∪B=A,求实数m的取值;
(2)若A∩B={x|0≤x≤3},求实数m的值;
(3)若A![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上函数![]() 的图象关于图象上点(1,0)对称,f(x)对任意的实数x都有
的图象关于图象上点(1,0)对称,f(x)对任意的实数x都有![]() 且f(3)=0,则函数y=f(x)在区间
且f(3)=0,则函数y=f(x)在区间![]() 上的零点个数最少有( )
上的零点个数最少有( )
A.2020个B.1768个C.1515个D.1514个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的偶函数f(x)和奇函数g(x)满足![]() .
.
(1)求函数f(x)和g(x)的表达式;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若方程![]() 在
在![]() 上恰有一个实根,求实数m的取值范围.
上恰有一个实根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() ,
,![]() ,
,![]() ,函数
,函数![]() ,
,![]() 的最小正周期为
的最小正周期为![]() .
.
(1)求![]() 的单调增区间;
的单调增区间;
(2)方程![]() ;在
;在![]() 上有且只有一个解,求实数n的取值范围;
上有且只有一个解,求实数n的取值范围;
(3)是否存在实数m满足对任意x1∈[-1,1],都存在x2∈R,使得![]() +
+![]() +m(
+m(![]() -
-![]() )+1>f(x2)成立.若存在,求m的取值范围;若不存在,说明理由.
)+1>f(x2)成立.若存在,求m的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知一动圆经过点
中,已知一动圆经过点![]() 且在
且在![]() 轴上截得的弦长为4,设动圆圆心的轨迹为曲线
轴上截得的弦长为4,设动圆圆心的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,
,![]() ,
,![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点
两点![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,求证:直线
,求证:直线![]() 过定点
过定点![]() ,并求出定点
,并求出定点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com