
【题目】某会议共出席![]() 个人
个人![]() ,其中每两个人都恰好同其余
,其中每两个人都恰好同其余![]() 个人相互问候过,对任何两个人,同这两个人都问候过的人数是相同的.问共有多少人出席会议?
个人相互问候过,对任何两个人,同这两个人都问候过的人数是相同的.问共有多少人出席会议?
【答案】36
【解析】
将人视为点,相识连线,毎点共组成![]() 个角,毎个角恰对应一个顶点,因此图中共有角
个角,毎个角恰对应一个顶点,因此图中共有角![]() 个.另一方面,设毎两个人,与该二人都相识的人有n个,因此对该二人对张n个角,毎角对应惟一一个二人,对毎二人对张且仅张有n个角, 从这一角度说总角数为
个.另一方面,设毎两个人,与该二人都相识的人有n个,因此对该二人对张n个角,毎角对应惟一一个二人,对毎二人对张且仅张有n个角, 从这一角度说总角数为![]() .
.
当然有![]() ,整理得
,整理得![]() ,其中n,k均为整数.易见
,其中n,k均为整数.易见![]() ,没n=3m,进一步化简得
,没n=3m,进一步化简得![]() ,即
,即![]() .当
.当![]() 时,
时,![]() ,
,![]() 不可能为整数.对于
不可能为整数.对于![]() ,
,
只有当k=3时,![]() 取整数,因此只可能是36人.
取整数,因此只可能是36人.
下面构造一个实例说明命题的情况存在.

如表R、O、Y、G、B、V表示6种颜色,将人染色,按上图排布,毎人恰好认识与他坐在同一行或同一列或与他具有相同顏色的人.这样,保证了毎人恰认识15个人,只需再证这种构造满足第二个条件即可.
设P、Q是任二个与会者,若他们坐在同一行,则与这两人都认识的人有这一行的其余4个人以及位于P所在列与Q同色的人,和位于Q所在列与P同色的人.当P、Q同色或位于同列均可类似地分析.假定P和Q不同行,不同列,且具有不同的颜色,则二人共同认识的6个人分别是:位于P所在的行和Q所在的列的1个人(与P、Q均不同色),位于p所在列和Q所在行的1个人,位于p所在行和列且与Q同色的2个人,位于Q所在行和列且与p同色的2个人.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() 平面
平面![]() ,点
,点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,且
的中点,且![]() ,
, ![]() .
.
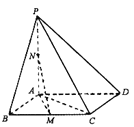
(1)证明: ![]() 平面
平面![]() ;
;
(2)设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,当
,当![]() 在
在![]() 内变化时,求二面角
内变化时,求二面角![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出三个游戏,袋子中分别装有若干只有颜色不同的小球(大小,形状,质量等均一样),从袋中无放回地取球,则其中不公平的游戏是______.
游戏1 | 游戏2 | 游戏3 | |
球数 | 3个黑球和一个白球 | 一个黑球和一个白球 | 2个黑球和2个白球 |
取法 | 取1个球,再取1个球 | 取1个球 | 取1个球,再取1个球 |
胜利 规则 | 取出的两个球同色→甲胜 | 取出的球是黑球→甲胜 | 取出的两个球同色→甲胜 |
取出的两个球不同色→乙胜 | 取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,点P
,点P![]() 在C上.
在C上.
(1)求椭圆C的方程;
(2)设![]() 分别为椭圆C的左右焦点,过
分别为椭圆C的左右焦点,过![]() 的直线
的直线![]() 与椭圆C交于不同的两点A、B,求△
与椭圆C交于不同的两点A、B,求△![]() 的内切圆的半径的最大值.
的内切圆的半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家“节能减排,开发清洁能源”的号召,小华制作了一个太阳灶,如图所示.集光板由抛物面(抛物线绕对称轴旋转得到)形的反光镜构成,已知镜口圆的直径为![]() ,镜深
,镜深![]() ,为达到最佳吸收太阳光的效果,容器灶圈应距离集光板顶点( )
,为达到最佳吸收太阳光的效果,容器灶圈应距离集光板顶点( )
A.0.5米B.1米C.1.5米D.2米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人2013-2017这五年的年度体检的血压值的折线图如图所示.
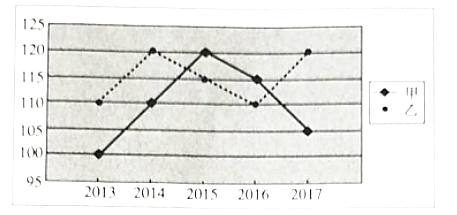
(1)根据散点图,直接判断甲、乙这五年年度体检的血压值谁的波动更大,并求波动更大者的方差;
(2)根据乙这五年年度体检血压值的数据,求年度体检血压值![]() 关于年份
关于年份![]() 的线性回归方程,并据此估计乙在2018年年度体检的血压值.
的线性回归方程,并据此估计乙在2018年年度体检的血压值.
(附: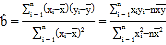 ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com