
| ξ | 0 | 1 | 2 | 3 |
| P | 0.12 | a | b | 0.12 |
| A |
. |
| B |
. |
| C |
| A |
. |
| B |
. |
| C |
. |
| B |
. |
| C |
. |
| A |
. |
| C |
. |
| A |
. |
| B |
. |
| C |
. |
| B |
. |
| A |


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 |
| 5 |
| ξ | 0 | 1 | 2 | 3 | ||||
| pi |
|
x | y |
|
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省高三第三次大考理科数学 题型:解答题
(本小题满分12分)从2003年开始,我国就通过实施高校自主招生探索人才选拔制度改革,允许部分高校拿出一定比例的招生名额,选拔那些有特殊才能的学生。某学生参加一个高校的自主招生考试,考试分笔试和面试两个环节,笔试有A、B两个题目,该学生答对A、B两题的概率分别为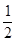 、
、 ,两题全部答对方可进入面试。面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为
,两题全部答对方可进入面试。面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为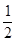 ,至少答对一题即可被录取。(假设每个环节的每个问题回答正确与否是相对独立的)
,至少答对一题即可被录取。(假设每个环节的每个问题回答正确与否是相对独立的)
(I)求该学生被学校录取的概率;
(II)设该学生答对题目的个数为ξ,求ξ的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
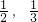 ,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对两个问题的概率均为
,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对两个问题的概率均为 ,至少答对一题即可被录取.(假设每个环节的每个问题回答正确与否是相对独立的).
,至少答对一题即可被录取.(假设每个环节的每个问题回答正确与否是相对独立的).查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省信阳高中高三第三次大考数学试卷(理科)(解析版) 题型:解答题
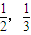 ,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对两个问题的概率均为
,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对两个问题的概率均为 ,至少答对一题即可被录取.(假设每个环节的每个问题回答正确与否是相对独立的).
,至少答对一题即可被录取.(假设每个环节的每个问题回答正确与否是相对独立的).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com