
【题目】在直角坐标系xOy中,曲线C的参数方程为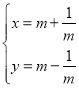 (m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
(m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线C和直线![]() 的直角坐标系方程;
的直角坐标系方程;
(2)已知![]() 直线
直线![]() 与曲线C相交于A,B两点,求
与曲线C相交于A,B两点,求![]() 的值.
的值.
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,需引进一条新的生产线投入生产,现有两条生产线可供选择,生产线①:有A,B两道独立运行的生产工序,且两道工序出现故障的概率依次是0.02,0.03.若两道工序都没有出现故障,则生产成本为15万元;若A工序出现故障,则生产成本增加2万元;若B工序出现故障,则生产成本增加3万元;若A,B两道工序都出现故障,则生产成本增加5万元.生产线②:有a,b两道独立运行的生产工序,且两道工序出现故障的概率依次是0.04,0.01.若两道工序都没有出现故障,则生产成本为14万元;若a工序出现故障,则生产成本增加8万元;若b工序出现故障,则生产成本增加5万元;若a,b两道工序都出现故障,则生产成本增加13万元.
(1)若选择生产线①,求生产成本恰好为18万元的概率;
(2)为最大限度节约生产成本,你会给工厂建议选择哪条生产线?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 与曲线
与曲线![]() 有两个公共点,求实数
有两个公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体![]() 中,面
中,面![]() 为矩形,面
为矩形,面![]() 面
面![]() ,
,![]() .
.
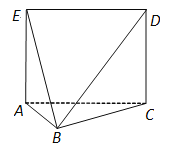
(1)求证:面![]() 面
面![]() ;
;
(2)已知多面体![]() 各顶点均在同一球面上,且该球的表面积为
各顶点均在同一球面上,且该球的表面积为![]() ,
,![]() ,当这个多面体的体积取得最大值时求其侧视图的面积.
,当这个多面体的体积取得最大值时求其侧视图的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() .以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线
.以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线![]() ,从原点O作射线交
,从原点O作射线交![]() 于点M,点N为射线OM上的点,满足
于点M,点N为射线OM上的点,满足![]() ,记点N的轨迹为曲线C.
,记点N的轨迹为曲线C.
(Ⅰ)求出直线![]() 的参数方程和曲线C的直角坐标方程;
的参数方程和曲线C的直角坐标方程;
(Ⅱ)设直线![]() 与曲线C交于P,Q两点,求
与曲线C交于P,Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新中国成立70周年以来,党中央国务院高度重视改善人民生活,始终把提高人民生活水平作为一切工作的出发点和落脚点城乡居民收入大幅增长,居民生活发生了翻天覆地的变化.下面是1949年及2015年~2018年中国居民人均可支配收入(元)统计图.以下结论中不正确的是( )

A.20l5年-2018年中国居民人均可支配收入与年份成正相关
B.2018年中居民人均可支配收入超过了1949年的500倍
C.2015年-2018年中国居民人均可支配收入平均超过了24000元
D.2015年-2018年中围居民人均可支配收入都超过了1949年的500倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() 是等边三角形,点
是等边三角形,点![]() 在棱
在棱![]() 上,平面
上,平面![]() 平面
平面![]() .
.
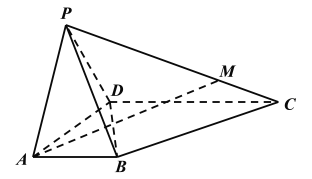
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值的最大值;
所成角的正弦值的最大值;
(3)设直线![]() 与平面
与平面![]() 相交于点
相交于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络商城在![]() 年
年![]() 月
月![]() 日开展“庆元旦”活动,当天各店铺销售额破十亿,为了提高各店铺销售的积极性,采用摇号抽奖的方式,抽取了
日开展“庆元旦”活动,当天各店铺销售额破十亿,为了提高各店铺销售的积极性,采用摇号抽奖的方式,抽取了![]() 家店铺进行红包奖励.如图是抽取的
家店铺进行红包奖励.如图是抽取的![]() 家店铺元旦当天的销售额(单位:千元)的频率分布直方图.
家店铺元旦当天的销售额(单位:千元)的频率分布直方图.

(1)求抽取的这![]() 家店铺,元旦当天销售额的平均值;
家店铺,元旦当天销售额的平均值;
(2)估计抽取的![]() 家店铺中元旦当天销售额不低于
家店铺中元旦当天销售额不低于![]() 元的有多少家;
元的有多少家;
(3)为了了解抽取的各店铺的销售方案,销售额在![]() 和
和![]() 的店铺中共抽取两家店铺进行销售研究,求抽取的店铺销售额在
的店铺中共抽取两家店铺进行销售研究,求抽取的店铺销售额在![]() 中的个数
中的个数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com