
【题目】已知向量  ,
, ![]() ,函数
,函数![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为
与其相邻的最高点的距离为![]() .
.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)计算![]() ;
;
(3)设函数![]() ,试讨论函数
,试讨论函数![]() 在区间
在区间![]() 上的零点个数.
上的零点个数.
【答案】(1) ![]() .(2) 2018. (3)当
.(2) 2018. (3)当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上无零点;当
上无零点;当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上有一个零点;当
上有一个零点;当![]() 时,函数
时,函数![]() 在
在![]() 有两个零点.
有两个零点.
【解析】试题分析:(1)根据平面向量数量积的坐标表示、二倍角公式和与辅助角公式可得![]() ,根据
,根据![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为
与其相邻的最高点的距离为![]() ,确定
,确定![]() ,从而根据正弦函数的单调性可得结果;(2)根据特殊角的三角函数及周期性可得结果;(3)
,从而根据正弦函数的单调性可得结果;(2)根据特殊角的三角函数及周期性可得结果;(3)![]() ,函数
,函数![]() 在区间
在区间![]() 上的零点个数,即为函数
上的零点个数,即为函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上的交点个数.在同一直角坐标系内作出这两个函数的图象,几何图形可得结果.
上的交点个数.在同一直角坐标系内作出这两个函数的图象,几何图形可得结果.
试题解析:(1) ![]() 向量
向量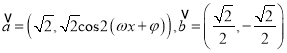 ,
, ![]() ,
, ![]() 点
点![]() 为函数
为函数![]() 图象上的一个最高点,
图象上的一个最高点, ![]() 点
点![]() 与其相邻的最高点的距离为
与其相邻的最高点的距离为![]() ,
, ![]() ,
, ![]() 函数
函数![]() 图象过点
图象过点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,由
,由![]() ,得
,得![]() ,
, ![]() 的单调增区间是
的单调增区间是![]() .
.
(2) 由(1)知![]() 的周期为
的周期为![]() ,且
,且![]() ,
, ![]() ,而
,而![]() .
.
(3) ![]() ,函数
,函数![]() 在区间
在区间![]() 上的零点个数,即为函数
上的零点个数,即为函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上的交点个数.在同一直角坐标系内作出这两个函数的图象如图所示,
上的交点个数.在同一直角坐标系内作出这两个函数的图象如图所示,

由图象可知,①当![]() 或
或![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上的无公共点,即函数
上的无公共点,即函数![]() 无零点;②当
无零点;②当![]() 与
与![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上有一个公共点,即函数
上有一个公共点,即函数![]() 有一个零点;③当
有一个零点;③当![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上有两个公共点,即函数
上有两个公共点,即函数![]() 有两个零点,综上,当
有两个零点,综上,当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上无零点;当
上无零点;当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上有一个零点;当
上有一个零点;当![]() 时,函数
时,函数![]() 在
在![]() 有两个零点.
有两个零点.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(Ⅰ)若![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(Ⅱ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅲ)若函数![]() 的图象与x轴交于A,B两点,线段AB中点的横坐标为
的图象与x轴交于A,B两点,线段AB中点的横坐标为![]() ,证明
,证明![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分15分)已知椭圆![]() :
:![]() 过点
过点![]() ,离心率为
,离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,过
的左、右焦点,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,记
,记![]() 的内切圆的面积为
的内切圆的面积为![]() ,求当
,求当![]() 取最大值时直线
取最大值时直线![]() 的方程,并求出最大值.
的方程,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):

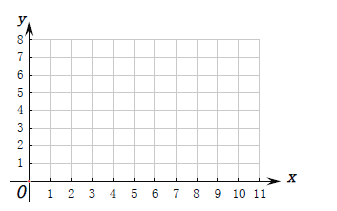
(Ⅰ)根据上表数据在下列网格中绘制散点图:
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)根据(Ⅱ)中的计算结果,若该商店准备一次性进货该商品![]() 吨,预测需要销售天数;
吨,预测需要销售天数;
参考公式和数据: 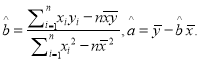
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(Ⅰ)根据以上数据建立一个2×2列联表;
(Ⅱ)能否在犯错误的概率不超过0.05的前提下认为性别与休闲方式有关系?
附: 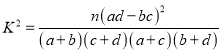
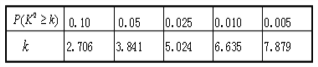
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]()
(Ⅰ)当点![]() 在
在![]() 轴上移动时,求点
轴上移动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 做直线
做直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,若在
两点,若在![]() 轴上存在一点
轴上存在一点![]() ,使得
,使得![]() 是以点
是以点![]() 为直角顶点的直角三角形,求直线
为直角顶点的直角三角形,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以
,以![]() 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,和平面内一点
,和平面内一点![]() ,过点
,过点![]() 任作直线
任作直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,设直线
两点,设直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试求
,试求![]() 满足的关系式.
满足的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com