
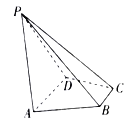
【题目】如图,在四棱锥![]() 中,
中, ![]() ,且
,且![]() .
.
(Ⅰ)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)当四棱锥![]() 的体积为
的体积为![]() ,且二面角
,且二面角![]() 为钝角时,求直线
为钝角时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由正三角形的性质可得
,由正三角形的性质可得![]() ,由勾股定理可得
,由勾股定理可得![]() ,根据线面垂直的判定定理可得
,根据线面垂直的判定定理可得![]() 平面
平面![]() ,从而根据面面垂直的判定定理可得平面
,从而根据面面垂直的判定定理可得平面![]() 平面
平面![]() ;(Ⅱ)根据四棱锥
;(Ⅱ)根据四棱锥![]() 的体积为
的体积为![]() ,可得
,可得![]() ,∴
,∴![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 为
为![]() 轴,
轴, ![]() 轴.在平面
轴.在平面![]() 内过点
内过点![]() 作垂直于平面
作垂直于平面![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,算出直线
,算出直线![]() 的方向向量与平面
的方向向量与平面![]() 的法向量,根据空间向量夹角的余弦公式可得结果.
的法向量,根据空间向量夹角的余弦公式可得结果.
试题解析:(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵![]() 为正三角形,∴
为正三角形,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴四边形![]() 为矩形,∴
为矩形,∴![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(Ⅱ)∵![]() ,
, ![]() ,
, ![]() ,
,
![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
∴过点![]() 作
作![]() 平面
平面![]() ,垂足
,垂足![]() 一定落在平面
一定落在平面![]() 与平面
与平面![]() 的交线
的交线![]() 上.
上.
∵四棱锥![]() 的体积为
的体积为![]() ,
,
∴![]()
![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
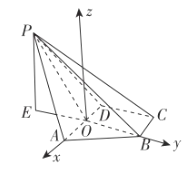
如图,以![]() 为坐标原点,以
为坐标原点,以![]() 为
为![]() 轴,
轴, ![]() 轴.
轴.
在平面![]() 内过点
内过点![]() 作垂直于平面
作垂直于平面![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
由题意可知![]() ,
, 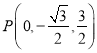 ,
, ![]() ,
, ![]() ,
, 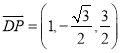 ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则![]() ,得
,得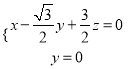 ,
,
令![]() ,则
,则![]() ,∴
,∴![]() ,
,
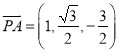 ,设直线
,设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则![]()
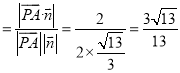 .
.
则直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【方法点晴】本题主要考查利用线面垂直、面面垂直的判定定理以及空间向量求线面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


科目:高中数学 来源: 题型:
【题目】设α,β为两个不同平面,a,b为两条不同直线,下列选项正确的是( )
①若a∥α,b∥α,则a∥b
②若aα,α∥β,则a∥β
③若α∥β,a∥β,则![]()
④若a∥α,则a与平面α内的无数条直线平行
⑤若a∥b,则a平行于经过b的所有平面
A.①②B.③④C.②④D.②⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学家欧拉在![]() 年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线后人称之为三角形的欧拉线.已知
年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线后人称之为三角形的欧拉线.已知![]() 的顶点
的顶点![]() 、
、![]() ,若其欧拉线方程为
,若其欧拉线方程为![]() ,则顶点
,则顶点![]() 的坐标是( )
的坐标是( )
参考公式:若![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 的坐标分别是
的坐标分别是![]() 、
、![]() 、
、![]() ,则该
,则该![]() 的重心的坐标为
的重心的坐标为![]() .
.
A.![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() ,有下列说法:
,有下列说法:
(1)函数![]() 满足
满足![]() 则函数在
则函数在![]() 上不是单调减函数;
上不是单调减函数;
(2)对任意的![]() 函数
函数![]() 满足
满足![]() 则函数在
则函数在![]() 上是单调增函数;
上是单调增函数;
(3)函数![]() 满足
满足![]() 则函数
则函数![]() 是偶函数;
是偶函数;
(4)函数![]() 满足
满足![]() 则函数
则函数![]() 不是奇函数.
不是奇函数.
其中,正确的说法是________(填写相应的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若不等式![]() 的解集是
的解集是![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,若不等式
时,若不等式![]() 对一切实数
对一切实数![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,设
时,设![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水产品经销商销售某种鲜鱼,售价为每公斤![]() 元,成本为每公斤
元,成本为每公斤![]() 元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价处理完,平均每公斤损失
元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价处理完,平均每公斤损失![]() 元.根据以往的销售情况,按
元.根据以往的销售情况,按![]() ,
,![]() ,
,![]() ,
,![]() ,
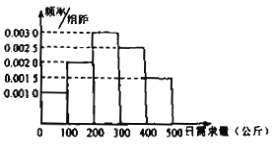
,![]() 进行分组,得到如图所示的频率分布直方图.
进行分组,得到如图所示的频率分布直方图.
(1)根据频率分布直方图计算该种鲜鱼日需求量的平均数![]() (同一组中的数据用该组区间中点值代表);
(同一组中的数据用该组区间中点值代表);
(2)该经销商某天购进了![]() 公斤这种鲜鱼,假设当天的需求量为
公斤这种鲜鱼,假设当天的需求量为![]() 公斤
公斤![]() ,利润为
,利润为![]() 元.求
元.求![]() 关于
关于![]() 的函数关系式,并结合频率分布直方图估计利润
的函数关系式,并结合频率分布直方图估计利润![]() 不小于
不小于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且a1=![]() ,an+1=Sn+
,an+1=Sn+![]() (n∈N*,t为常数).
(n∈N*,t为常数).
(Ⅰ)若数列{an}为等比数列,求t的值;
(Ⅱ)若t>﹣4,bn=lgan+1,数列{bn}前n项和为Tn,当且仅当n=6时Tn取最小值,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com