
(本小题14分)
(I)已知数列 满足
满足
 ,
, 满足
满足 ,
,
 ,求证:
,求证: 。.
。.
(II) 已知数列 满足:a
满足:a =1且
=1且 。设m
。设m N
N ,m
,m n
n 2,证明(a
2,证明(a +
+ )
) (m-n+1)
(m-n+1)


证明:
(I)记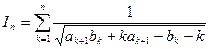 ,则
,则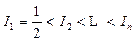 。 …… 2分
。 …… 2分
而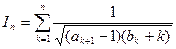
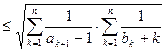 。 ……………… 4分
。 ……………… 4分
因为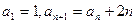 ,所以
,所以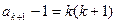 。 ………………… 5分
。 ………………… 5分
从而有 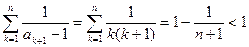 。 ①
。 ①
又因为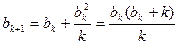 ,所以
,所以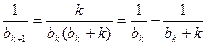 ,
,
即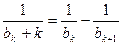 。从而有
。从而有 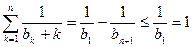 。② … 6分
。② … 6分
由(1)和(2)即得  。综合得到
。综合得到 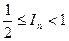 。
。
左边不等式的等号成立当且仅当 n=1时成立。 ……… 7分
(II)不妨设 即
即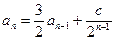 与
与 比较系数得c=1.即
比较系数得c=1.即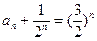

又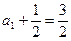 ,故{
,故{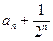 }是首项为
}是首项为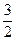 公比为
公比为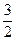 的等比数列,
的等比数列,
故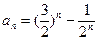 ……… 10分
……… 10分
这一问是数列、二项式定理及不等式证明的综合问题.综合性较强.
即证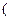
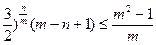 ,当m=n时显然成立。易验证当且仅当m=n=2时,等号成立。
,当m=n时显然成立。易验证当且仅当m=n=2时,等号成立。
设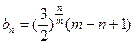 下面先研究其单调性。当
下面先研究其单调性。当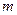 >n时,
>n时,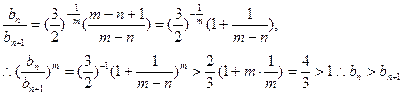 ……… 12分
……… 12分
即数列{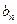 }是递减数列.因为n
}是递减数列.因为n 2,故只须证
2,故只须证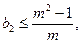 即证
即证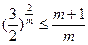 。事实上,
。事实上,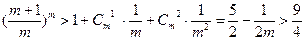 故上不等式成立。综上,原不等式成立。 ……………… 14分
故上不等式成立。综上,原不等式成立。 ……………… 14分
解析


 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源:2010-2011年海南省嘉积中学高二下学期质量检测数学理卷(一) 题型:填空题
((本小题14分)
已知函数
(I)若函数 在
在 时取得极值,求实数
时取得极值,求实数 的值;
的值;
(II)试讨论函数 的单调性;
的单调性;
查看答案和解析>>
科目:高中数学 来源:2014届福建省高二上学期期中考试文科数学试题(解析版) 题型:解答题
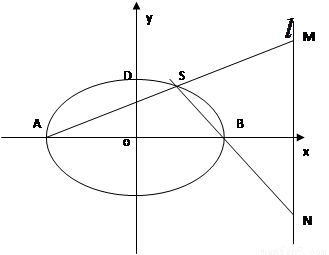
(本小题14分)已知直线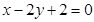 经过椭圆
经过椭圆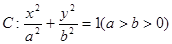 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆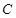 的右顶点为
的右顶点为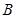 ,点
,点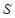 是椭圆
是椭圆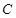 上位于
上位于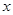 轴上方的动点,直线
轴上方的动点,直线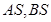 与直线
与直线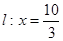 分别交于
分别交于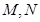 两点。
两点。
(I)求椭圆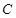 的方程;
的方程;
(Ⅱ)求线段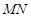 的长度的最小值;
的长度的最小值;
(Ⅲ)当线段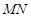 的长度最小时,在椭圆
的长度最小时,在椭圆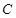 上是否存在这样的点
上是否存在这样的点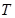 ,使得
,使得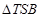 的面积为
的面积为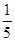 ?若存在,确定点
?若存在,确定点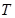 的个数,若不存在,说明理由。
的个数,若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源:2010-2011年海南省高二下学期质量检测数学理卷(一) 题型:填空题
((本小题14分)
已知函数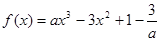
(I)若函数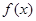 在
在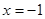 时取得极值,求实数
时取得极值,求实数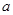 的值;
的值;
(II)试讨论函数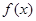 的单调性;
的单调性;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com