
【题目】已知函数f(x)=ex+ ![]() (a∈R)是定义域为R的奇函数,其中e是自然对数的底数.
(a∈R)是定义域为R的奇函数,其中e是自然对数的底数.
(1)求实数a的值;
(2)若存在x∈(0,+∞),使不等式f(x2+x)+f(2﹣tx)<0成立,求实数t的取值范围;
(3)若函数y=e2x+ ![]() ﹣2mf(x)在(m,+∞)上不存在最值,求实数m的取值范围.
﹣2mf(x)在(m,+∞)上不存在最值,求实数m的取值范围.
【答案】
(1)解:因为 ![]() 在定义域R上是奇函数,
在定义域R上是奇函数,
所以 ![]()
即 ![]() 恒成立,
恒成立,
所以a=﹣1,此时 ![]()
(2)解:因为f(x2+x)+f(2﹣tx)<0
所以f(x2+x)<﹣f(2﹣tx)
又因为 ![]() 在定义域R上是奇函数,
在定义域R上是奇函数,
所以f(x2+x)<f(tx﹣2)
又因为 ![]() 恒成立
恒成立
所以 ![]() 在定义域R上是单调增函数
在定义域R上是单调增函数
所以存在x∈(0,+∞),使不等式f(x2+x)+f(2﹣tx)<0成立
等价于存在x∈(0,+∞),x2+x<tx﹣2成立,
所以存在x∈(0,+∞),使(t﹣1)x>x2+2,即 ![]()
又因为 ![]() ,当且仅当
,当且仅当 ![]() 时取等号
时取等号
所以 ![]() ,即
,即 ![]() ,
,
注:也可令g(x)=x2﹣(t﹣1)x+2
①对称轴 ![]() 时,即t≤1g(x)=x2﹣(t﹣1)x+2在x∈(0,+∞)是单调增函数的.
时,即t≤1g(x)=x2﹣(t﹣1)x+2在x∈(0,+∞)是单调增函数的.
由g(0)=2>0不符合题意
②对称轴 ![]() 时,即t>1
时,即t>1
此时只需△=(t﹣1)2﹣8≥0得 ![]() 或者
或者 ![]()
所以 ![]()
综上所述:实数t的取值范围为 ![]()
(3)解:函数 ![]()
令 ![]()
则 ![]() 在x∈(m,+∞)不存在最值等价于函数y=t2﹣2mt+2,
在x∈(m,+∞)不存在最值等价于函数y=t2﹣2mt+2,
在 ![]() 上不存在最值,
上不存在最值,
由函数y=t2﹣2mt+2,的对称轴为t0=m得: ![]() 成立,
成立,
令 ![]()
由 ![]()
所以 ![]() 在m∈R上是单调增函数.
在m∈R上是单调增函数.
又因为g(0)=0,
所以实数m的取值范围为m>0
【解析】(1)根据题意,由奇函数的性质可得以 ![]() ,解可得a的值;(2)由函数为奇函数可得f(x2+x)<f(tx﹣2),对f(x)求导分析可得f(x)为增函数,进而分析可以将不等式f(x2+x)+f(2﹣tx)<0转化为存在x∈(0,+∞),x2+x<tx﹣2成立,由基本不等式的性质分析可得答案.(3)根据题意,计算可得y=e2x+
,解可得a的值;(2)由函数为奇函数可得f(x2+x)<f(tx﹣2),对f(x)求导分析可得f(x)为增函数,进而分析可以将不等式f(x2+x)+f(2﹣tx)<0转化为存在x∈(0,+∞),x2+x<tx﹣2成立,由基本不等式的性质分析可得答案.(3)根据题意,计算可得y=e2x+ ![]() ﹣2mf(x)的解析式,用换元法分析可得y=t2﹣2mt+2,在
﹣2mf(x)的解析式,用换元法分析可得y=t2﹣2mt+2,在 ![]() 上不存在最值,由二次函数的性质分析可得答案.
上不存在最值,由二次函数的性质分析可得答案.
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.


科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的奇函数,且对任意a、b∈R,当a+b≠0时,都有 ![]() .
.
(1)若a>b,试比较f(a)与f(b)的大小关系;
(2)若f(1+m)+f(3-2m)≥0,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论不正确的是(填序号).
①各个面都是三角形的几何体是三棱锥;
②以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥;
③棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥;
④圆锥的顶点与底面圆周上的任意一点的连线都是母线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,AB=AC=AA1 , AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动. 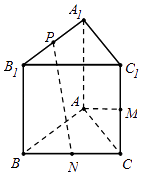
(Ⅰ)求证:PN⊥AM;
(Ⅱ)试确定点P的位置,使直线PN和平面ABC所成的角最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的图象关于y轴对称,当x∈(0,+∞)时,f(x)=log2x,若a=f(﹣3),b=f( ![]() ),c=f(2),则a,b,c的大小关系是( )
),c=f(2),则a,b,c的大小关系是( )
A.a>b>c
B.b>a>c
C.c>a>b
D.a>c>b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com