
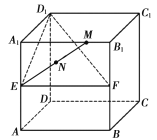
【题目】在棱长为2的正方体![]() 中,
中,![]() ,
,![]() 分别为棱
分别为棱![]() 、
、![]() 的中点,
的中点,![]() 为棱
为棱![]() 上的一点,且
上的一点,且![]() ,设点
,设点![]() 为
为![]() 的中点,则点
的中点,则点![]() 到平面
到平面![]() 的距离为( )
的距离为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
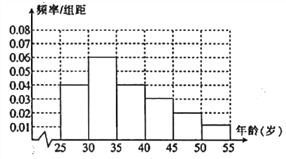
【题目】某高校进行社会实践,对![]() 岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在
岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在![]() 岁,
岁, ![]() 岁年龄段人数中,“时尚族”人数分别占本组人数的
岁年龄段人数中,“时尚族”人数分别占本组人数的![]() 、
、![]() .
.
(1)求![]() 岁与
岁与![]() 岁年龄段“时尚族”的人数;
岁年龄段“时尚族”的人数;
(2)从![]() 岁和
岁和![]() 岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在
岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在![]() 岁内的概率。
岁内的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为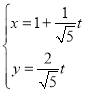 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次田径比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示。

若将运动员按成绩由好到差编为1—35号,再用系统抽样方法从中抽取5人,则其中成绩在区间![]() 上的运动员人数为
上的运动员人数为
A.6B.5C.4D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计,某蔬菜基地西红柿亩产量的增加量![]() (百千克)与某种液体肥料每亩使用量
(百千克)与某种液体肥料每亩使用量![]() (千克)之间的对应数据的散点图,如图所示.
(千克)之间的对应数据的散点图,如图所示.
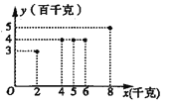
(1)依据数据的散点图可以看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(若
并加以说明(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)求![]() 关于
关于![]() 的回归方程,并预测液体肥料每亩使用量为12千克时,西红柿亩产量的增加量
的回归方程,并预测液体肥料每亩使用量为12千克时,西红柿亩产量的增加量![]() 约为多少?
约为多少?
附:相关系数公式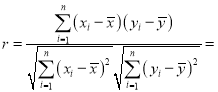
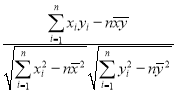 ,参考数据:
,参考数据:![]() ,
,![]() .
.
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: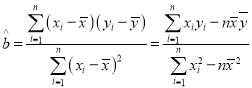 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班共有![]() 名学生,已知以下信息:
名学生,已知以下信息:
①男生共有![]() 人;
人;
②女团员共有![]() 人;
人;
③住校的女生共有![]() 人;
人;
④不住校的团员共有![]() 人;
人;
⑤住校的男团员共有![]() 人;
人;
⑥男生中非团员且不住校的共有![]() 人;
人;
⑦女生中非团员且不住校的共有![]() 人.
人.
根据以上信息,该班住校生共有______人![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com