
分析 根据题意,作图分析可得AD=2和AC=2$\sqrt{3}$,进而由数量积的计算公式可得AG=$\sqrt{3}$,即G是AC的中点,则有$\overrightarrow{AC}$=2$\overrightarrow{AG}$,由平面向量基本定理可得$\overrightarrow{AG}$=$λ\overrightarrow{AM}$+$μ\overrightarrow{AN}$,(λ+μ=1),结合题意分析可得m=2λ,n=2μ,故有m+n=2;进而分析可得$\frac{1}{m}+\frac{1}{n+1}$=$\frac{1}{3}$×($\frac{1}{m}+\frac{1}{n+1}$)(m+n+1),由基本不等式分析可得答案.
解答 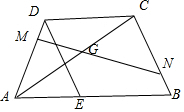 解:根据题意,如图:作DE∥BC,由于∠A=60°,且AE=AB-CD=2,
解:根据题意,如图:作DE∥BC,由于∠A=60°,且AE=AB-CD=2,
则有AD=2,
又由∠ADC=120°,则有AC=2$\sqrt{3}$,
同时有∠CAD=∠CAB=30°,
若$\overrightarrow{AG}•\overrightarrow{AB}$=6,则有$\overrightarrow{AG}•\overrightarrow{AB}$=|$\overrightarrow{AG}$||$\overrightarrow{AB}$|cos∠CAB=6,
则由AG=$\sqrt{3}$,即G是AC的中点,
则有$\overrightarrow{AC}$=2$\overrightarrow{AG}$,
又由G、M、N三点共线,则有$\overrightarrow{AG}$=$λ\overrightarrow{AM}$+$μ\overrightarrow{AN}$,(λ+μ=1),
而$\overrightarrow{AC}$=2$\overrightarrow{AG}$且$\overrightarrow{AC}$=m$\overrightarrow{AM}+n\overrightarrow{AN}$,
则有m=2λ,n=2μ,
故有m+n=2;
$\frac{1}{m}+\frac{1}{n+1}$=$\frac{1}{3}$×($\frac{1}{m}+\frac{1}{n+1}$)(m+n+1)=$\frac{1}{3}$×[2+$\frac{n+1}{m}$+$\frac{m}{n+1}$]≥$\frac{4}{3}$,
即$\frac{1}{m}+\frac{1}{n+1}$的最小值为$\frac{4}{3}$;
故答案为:$\frac{4}{3}$.
点评 本题考查基本不等式的运用,涉及三角形的几何计算以及平面向量的加法运算以及数量积的运算,关键是分析得到G为AC的中点.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | [$\frac{1}{2}$,2] | C. | (0,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {2} | C. | {2,5} | D. | [2,$\sqrt{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<ef(0),f(2016)>e2016f(0) | B. | f(1)>ef(0),f(2016)>e2016f(0) | ||
| C. | f(1)>ef(0),f(2016)<e2016f(0) | D. | f(1)<ef(0),f(2016)<e2016f(0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com