
指出下列推理的两个步骤分别遵循哪种推理规则?
如图,因为四边形ABCD是平行四边形.
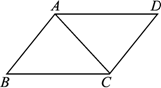
所以AB=CD,BC=AD.
又因为△ABC和△CDA的三边对应相等.
所以△ABC≌△CDA.
探究:这个证明过程包含着两个三段论推理.在第一个推理中,暗含着一个一般性原理“平行四边形的对边相等”,这个已被证明了的一般定理是大前提,“四边形ABCD是平等四边形”是小前提,把一般性原理用于前面的具体情况,于是得到结论“AB=CD,BC=AD”,在第二个推理中,大前提是已被证明了的一般定理“有三边对应相等的两个三角形全等”,小前提是AB=CD,BC=AD,AC=CA,结论是△ABC≌△CDA.
规律总结:数学中的演绎法一般是以三段论式的格式进行的,三段论是由三个判断组成的,其中两个为前提,另一个是结论,第一个判断是提供性质的一般判断,叫做大前提,通常是已知的公理、定理、定义.如上例中的两个大前提分别是“平行四边形的对边相等”和“有三边对应相等的两个三角形全等”;第二个判断是和大前提有联系的特殊判断,叫做小前提,通常是已知条件或前面推理的第三个判断.如上例中的两个小前提分别是“四边形ABCD是平等四边形”(已知条件)和“△ABC和△CDA的三边对应相等”(前面推理的第三个判断);第三个判断叫做结论,是联合前两个判断,根据它们的联系作出的新判断,如上例中的两个结论分别是“AB=CD,BC=AD”和“△ABD≌△CDA”.
在推理论证的过程中,一个稍复杂一点的证明题经常要由几个三段论式才能完成,大前提通常省略不写,或者写在结论后面的括号内,小前提有时也可以省去,而采取某种简明的推理格式.


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
| 2 |
| 2 |
| M1F1 |
| M1F |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高二版(A选修1-2) 2009-2010学年 第30期 总第186期 人教课标版(A选修1-2) 题型:044
指出下列推理的两个步骤分别遵循哪种推理规则?
如下图,因为四边形ABCD是平行四边形,所以AB=CD,BC=AD.

又因为△ABC和△CDA的三边对应相等,所以△ABC≌△CDA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com