
分析 (1)化小数为分数,化负指数为正指数,然后利用有理指数幂的运算性质化简求值;
(2)直接利用对数的运算性质化简求值.
解答 解:(1)($\frac{27}{8}$)${\;}^{-\frac{2}{3}}$-($\frac{49}{9}$)0.5+(0.008)${\;}^{-\frac{2}{3}}$×$\frac{2}{25}$
=$[(\frac{3}{2})^{3}]^{-\frac{2}{3}}-[(\frac{7}{3})^{2}]^{\frac{1}{2}}+[(\frac{1}{5})^{3}]^{-\frac{2}{3}}×\frac{2}{25}$
=$\frac{4}{9}-\frac{7}{3}+2=\frac{1}{9}$;
(2)$\frac{lg5•lg8000+(lg{2}^{\sqrt{3}})^{2}}{lg600-\frac{1}{2}lg0.036-\frac{1}{2}lg0.1}$=$\frac{lg5•(lg8+3)+(\sqrt{3}lg2)^{2}}{lg6+2-\frac{1}{2}lg\frac{36}{1000}-\frac{1}{2}lg\frac{1}{10}}$
=$\frac{lg5•(3lg2+3)+3(lg2)^{2}}{lg6+2+\frac{1}{2}(2lg6-3)+\frac{1}{2}}$=$\frac{3lg5•lg2+3lg5+3(lg2)^{2}}{4}$
=$\frac{3lg2(lg5+lg2)+3lg5}{4}$=$\frac{3lg2+3lg5}{4}=\frac{3}{4}$.
点评 本题考查对数的运算性质,考查了有理指数幂的化简求值,是基础的计算题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 240 | C. | 360 | D. | 480 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6x-y-4=0 | B. | 6x-y+4=0 | C. | 6x+y+4=0 | D. | 6x+y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
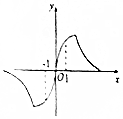
| A. | (1,+∞) | B. | (-2,-1) | C. | (-2,0) | D. | (-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
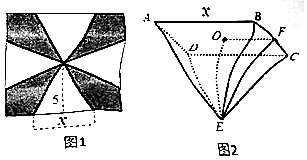
| A. | $\frac{25\sqrt{3}}{6}$ | B. | $\frac{50}{3}$ | C. | $\frac{25}{3}$ | D. | $\frac{125\sqrt{3}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com