
 的符号.
的符号. 的集合,根据k取偶数和奇数两种情况,分别判断sin
的集合,根据k取偶数和奇数两种情况,分别判断sin 和cos
和cos 的符号,进而得到式子
的符号,进而得到式子 的符号.
的符号.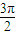 (k∈Z),
(k∈Z), <
< <kπ+
<kπ+ (k∈Z).
(k∈Z).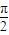 <
< <2nπ+
<2nπ+ ,此时
,此时 在第二象限,
在第二象限, >0,cos
>0,cos <0,∴
<0,∴ <0.
<0.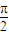 <
< <(2n+1)π+
<(2n+1)π+ (n∈Z),
(n∈Z),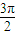 <
< <2nπ+
<2nπ+ (n∈Z),此时
(n∈Z),此时 在第四象限.
在第四象限. <0,cos
<0,cos >0,因此
>0,因此 <0,
<0, <0.
<0. 的象限,再根据“一全正、二正弦、三正切、四余弦”来判断三角函数值的符号.
的象限,再根据“一全正、二正弦、三正切、四余弦”来判断三角函数值的符号. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com