练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm，如果不计容器的厚度，则球的体积为（　　）
    A、
    500π
    3
     cm3
    B、
    866π
    3
     cm3
    C、
    1372π
    3
     cm3
    D、
    2048π
    3
     cm3
    考点：球的体积和表面积
    专题：计算题,空间位置关系与距离
    分析：设正方体上底面所在平面截球得小圆M，可得圆心M为正方体上底面正方形的中心．设球的半径为R，根据题意得球心到上底面的距离等于（R-2）cm，而圆M的半径为4，由球的截面圆性质建立关于R的方程并解出R=5，用球的体积公式即可算出该球的体积．
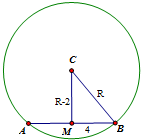    解答： 解：设正方体上底面所在平面截球得小圆M，
    则圆心M为正方体上底面正方形的中心．如图．
    设球的半径为R，根据题意得球心到上底面的距离等于（R-2）cm，而圆M的半径为4，由球的截面圆性质，得R2=（R-2）2+42，
    解出R=5，
    ∴根据球的体积公式，该球的体积V=
    4π
    3
    R3    =
    500π
    3
    cm3．
    故选A．
    点评：本题给出球与正方体相切的问题，求球的体积，着重考查了正方体的性质、球的截面圆性质和球的体积公式等知识，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某空间几何体的三视图如图所示，则该几何体的体积为（　　）
    A、1200+72π
    B、B、1200+144π
    C、1600+72π
    D、1600+144π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

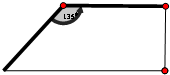    两直立矮墙成135°二面角，现利用这两面矮墙和篱笆围成一个面积为54m2的直角梯形菜园（墙足够长），已知修筑篱笆每米的费用为50元，则修筑这个菜园的最少费用为为
     
    元．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知[x]表示不超过实数x的最大整数，例如[1.3]=1，[-2.6]=-3，g（x）=[x]为取整函数，已知x0是函数f（x）=lnx-
    2
    x
     的零点，则g（x0）等于（　　）
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对某中学高二年级学生是爱好体育还是爱好文娱进行调查，共调查了50人，所得2×2列联表如下：
    爱好
    体育    		爱好
    文娱    		合计
    男生15AB
    女生C10D
    合计20E50
    （1）求出2×2列联表中A、B、C、D、E的值；
    （2）若已选出指定的三个男生甲、乙、丙；两个女生M，N，现从中选两人参加某项活动，求选出的两个人恰好是一男一女的概率；
    （3）试用独立性检验方法判断性别与爱好体育关系？
    参考公式：①K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)

    ②独立性检验概率表
    P（K2≥k）0.500.400.250.150.100.050.0250.0100.0050.001
    k0.4550.7081.3232.0722.7063.845.0246.6357.87910.83

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列各式中，值为0.5是（　　）
    A、sin15°cos15°
    B、
    tan22.5°
    1-tan222.5°
    C、cos2
    π
    12
    sin2
    π
    12
    D、
    1
    2
    +
    1
    2
    cos
    π
    6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）的定义域为（0，+∞），对任意x1，x2∈（0，+∞）都有f（
    x1
    x2
    ）=f（x1）-f（x2），且当x＞1时，f（x）＞0．
    （Ⅰ）求f（1）的值；
    （Ⅱ）求证：f（x）在（0，+∞）上是增函数；
    （Ⅲ）若f（2）=1，求不等式f（x）-f（
    1
    x-3
    ）≤2的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数y=ax+1在[1，2]上的最大值与最小值的差为2，则实数a的值是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    不等式x2+ax+4＜0的解集不是空集，则实数a的取值范围是（　　）
    A、（-∞，-4）∪（4，+∞）
    B、（-4，4）
    C、（-∞，-4]∪[4，+∞）
    D、[-4，4]

    查看答案和解析>>

    同步练习册答案