
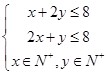 ,目标函数z=3x+y,某学生求得x=
,目标函数z=3x+y,某学生求得x=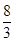 , y=
, y=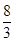 时,
时,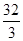 , 这显然不合要求,正确答案应为( )
, 这显然不合要求,正确答案应为( ) | A.x="3," y="3" , zmax="12" | B.x="3," y="2" , zmax=11. |
| C.x="2," y=" 3" , zmax= 9. | D.x="4," y=" 0" , zmax= 12. |
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
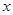 亩水稻,
亩水稻,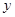 亩花生,利润
亩花生,利润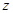 元,请写出约束条件及目标函数;(2)问两种作物各种多少,才能获得最大收益?
元,请写出约束条件及目标函数;(2)问两种作物各种多少,才能获得最大收益?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com