
(12分)在梯形ABCD中AB∥CD,AD=DC=CB=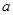 ,
,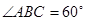 ,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=
,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=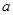 .
.
(1)求证:BC⊥平面ACFE;
(2)求EC与平面BEF所成角的正弦值.

.(1) ∵AB∥CD,AD=DC=CB=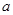 ,
,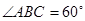
∴梯形ABCD为等腰梯形,AB=2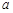 .
.
三角形ACB中,∠ABC=60°,CB=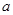 ,AB=2
,AB=2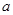
∴ AC=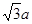 ,∠ACB=90°即BC⊥AC
.................3分
,∠ACB=90°即BC⊥AC
.................3分
又∵平面ACFE⊥平面ABCD,
平面ACFE∩平面ABCD=AC
∴ BC⊥平面ACFE. ..........................6分
(2)取B、F中点H,连结C、H.

∵BC⊥平面ACFE, EF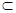 平面ACFE
平面ACFE
∴BC⊥EF
又EF⊥FC , ∴EF⊥平面BCF
∵EF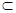 平面BEF
平面BEF
∴平面BEF⊥平面BCF
又等腰△BCF中,CH⊥BF
∴CH⊥平面BEF,即∠CEH为所求角。 ……………9分
Rt△CHE中,CH=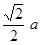 ,EC=2
,EC=2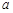
sin∠CEH=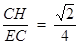 .
..........................`12分
.
..........................`12分
【解析】略


科目:高中数学 来源: 题型:
(08年黄冈中学一模文) (12分) 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a , ∠ABC=60°.平面ACEF⊥平面ABCD,且四边形ACEF是矩形,AF=a.
(I)求证:AC⊥BE;
(II)求二面角B-EF-D的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
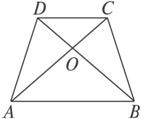
图1-21
查看答案和解析>>
科目:高中数学 来源:2012年北师大版高中数学必修5 2.1正余弦定理练习卷(解析版) 题型:解答题
如图所示,已知在梯形ABCD中AB∥CD,CD=2, AC=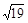 ,∠BAD=
,∠BAD= ,求梯形的高.
,求梯形的高.

查看答案和解析>>
科目:高中数学 来源:2010年辽宁省高二下学期第一次月考数学(理) 题型:选择题
如图,在梯形ABCD中,AB//DC,AB=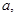
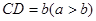 。若
。若
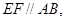 EF到CD与AB的距离之比为
EF到CD与AB的距离之比为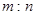 ,则可推算出:
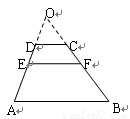
,则可推算出: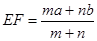 ,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设
,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设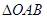 ,
,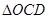 的面积分别为
的面积分别为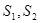 ,EF//AB,且EF到CD与AB的距离之比为
,EF//AB,且EF到CD与AB的距离之比为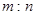 ,则
,则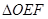 的面积
的面积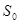 与
与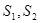 的关系是( )
的关系是( )
A.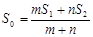 B.
B.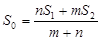
C.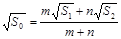 D.
D.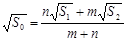
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com