

分析 (1)证明BD⊥平面ACP,可得BD⊥AP,利用DE⊥AP,BD∩DE=D,即可证明AP⊥平面BDE;
(2)证明DF∥AP,利用AP⊥平面BDE,可得DF⊥平面BDE,即可证明平面BDF⊥平面BDE;
(3)利用平面与平面平行的判定,即可得出结论.
解答 (1)证明:∵D为AC的中点,AB=BC,∴BD⊥AC,
∵把平面四边形ABCP沿AC折成直二面角,
∴平面ACP⊥平面ABC,平面ACP∩平面ABC=AC,
∴BD⊥平面ACP,
∵AP?平面ACP,
∴BD⊥AP,
∵DE⊥AP,BD∩DE=D,
∴AP⊥平面BDE;
(2)证明:∵D,F分别为AC,PC的中点,
∴DF∥AP,
∵AP⊥平面BDE,
∴DF⊥平面BDE,
∵DF?平面BDF,
∴平面BDF⊥平面BDE;
(3)解:存在点Q,使得平面CHQ∥平面BDE,此时AE=EQ.
点评 本题考查线面、面面垂直,考查面面平行,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
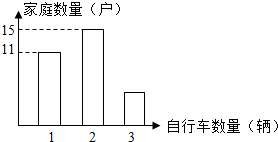 某个小区为了制订自行车棚的整修方案,进行了一次以家庭为单位的自行车数量调查.按照家庭成员的人数采用分层抽样的方法,一部分数据如表所示,其中m=2n.通过调查统计了每个家庭的自行车数量,将结果绘制成条形图,如图所示.
某个小区为了制订自行车棚的整修方案,进行了一次以家庭为单位的自行车数量调查.按照家庭成员的人数采用分层抽样的方法,一部分数据如表所示,其中m=2n.通过调查统计了每个家庭的自行车数量,将结果绘制成条形图,如图所示.| 家庭人数 | 1 | 2 | 3 | 4 | 5 |
| 家庭数量 | 6 | m | 72 | 18 | |
| 抽样数量 | 4 | n | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 1期投入1亿元 | 建垃圾堆肥厂 | 造有机肥十多万吨 | 年收益2千万元 |
| 2期投入4亿元 | 建焚烧发电1厂 | 年发电1.3亿kw | 年收益4千万元 |
| 3期投入2亿元 | 建焚烧发电2厂 | 年发电1.3亿kw | 年收益4千万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com