【题目】在平面直角坐标系
中，设中心在坐标原点，焦点在
轴上的椭圆
的左、右焦点分别为
，右准线
与轴的交点为
，
.
（1）已知点
在椭圆上，求实数
的值；
（2）已知定点
．
① 若椭圆上存在点
，使得
，求椭圆的离心率的取值范围；
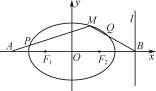
② 如图，当
时，记
为椭圆上的动点，直线
分别与椭圆交于另一点
，若
且
，求证：
为定值．
【答案】（1）2；（2）见解析
【解析】
（1）由椭圆的准线方程列式求解；
（2）①设点T（x，y）由
，得（x+2）2+y2=2[（x+1）2+y2]，即x2+y2=2．得出关于m的关系式求得离心率范围；
②设M（x0，y0），P（x1，y1），Q（x2，y2）由
=λ
，
=μ
的关系列式求解．
（1）设椭圆的标准方程为
，则
，
所以
，椭圆的标准方程为
，代入点
，
解得
（舍负）.（先求标准方程也可）
（2）①点
坐标为
，设点
坐标为
，由，
得
，化简，得
，
与椭圆方程联立，得
，而
，则
解得
，离心率
，
（也可以从长半轴短半轴与圆的半径关系求
的范围）
所以，椭圆
的离心率的取值范围为
.
②设点
的坐标分别为
，则
，由
得
，则
，
代入
，整理得
，而
，则
，而由题意，显然
，
则
，所以
；
同理，由
得，
，
所以，
.
科目：高中数学 来源： 题型：
【题目】在(2x-3y)10的展开式中,求:
(1)各项的二项式系数的和;
(2)奇数项的二项式系数的和与偶数项的二项式系数的和;
(3)各项系数之和;
(4)奇数项系数的和与偶数项系数的和.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某大学为调查来自南方和北方的同龄大学生的身高差异，从2016级的年龄在18～19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名，测量他们的身高，量出的身高如下(单位：cm)：
南方：158，170，166，169，180，175，171，176，162，163.
北方：183，173，169，163，179，171，157，175，184，166.
(1)根据抽测结果，画出茎叶图，对来自南方和北方的大学生的身高作比较，写出统计结论．
(2)设抽测的10名南方大学生的平均身高为
cm，将10名南方大学生的身高依次输入如图所示的程序框图进行运算，问输出的s大小为多少？并说明s的统计学意义。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是边长为4的正方形，PA⊥平面ABCD，E为PB中点，PB=4
．
（I）求证：PD∥面ACE；
（Ⅱ）求三棱锥E﹣ABC的体积。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC= 
AD，∠BAD=∠ABC=90°． （Ⅰ）证明：直线BC∥平面PAD；
（Ⅱ）若△PAD面积为2 
，求四棱锥P﹣ABCD的体积．
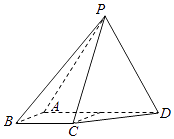
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设有下面四个命题
p1：若复数z满足 
∈R，则z∈R；
p2：若复数z满足z2∈R，则z∈R；
p3：若复数z1 ， z2满足z1z2∈R，则z1= 
；
p4：若复数z∈R，则 
∈R．
其中的真命题为（ ）
A.p1 ， p3
B.p1 ， p4
C.p2 ， p3
D.p2 ， p4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念，记交通指数为T．其
范围为[0，10]，分别有五个级别：T∈[0，2）畅通;T∈[2，4)基本畅通; T∈[4，6）轻度拥堵; T∈[6，8)中度拥堵；T∈[8，10]严重拥堵，晚高峰时段(T≥2)，从某市交通指挥中心选取了市区20个交通路段，依据其交通指数数据绘制的部分直方图如图所示．
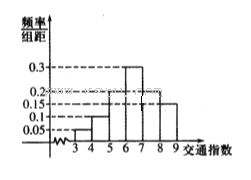
(1)请补全直方图，并求出轻度拥堵、中度拥堵、严重拥堵路段各有多少个？
(2)用分层抽样的方法从交通指数在[4，6），[6，8），[8，l0]的路段中共抽取6个路段，求依次抽取的三个级别路段的个数；
(3)从(2)中抽出的6个路段中任取2个，求至少一个路段为轻度拥堵的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
