
设集合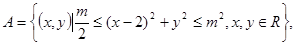
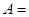
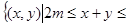
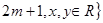 .若
.若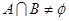 ,则实数
,则实数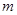 的取值范围是_____________。
的取值范围是_____________。
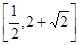
【解析】
试题分析:由题意可知,当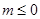 时,
时,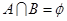 ,所以
,所以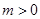 ,所以可知集合
,所以可知集合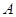 表示圆心为
表示圆心为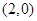 的“圆环”,大圆半径为
的“圆环”,大圆半径为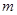 ,小圆半径为
,小圆半径为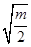 ;集合
;集合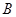 表示两条平行的直线所夹部分,画出图形后,观察
表示两条平行的直线所夹部分,画出图形后,观察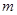 的变化范围使得
的变化范围使得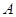 和
和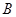 有交集即可得到结果。
有交集即可得到结果。
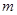 从0开始增大,增大到约1/4时,有一条直线和大圆相切,此后
从0开始增大,增大到约1/4时,有一条直线和大圆相切,此后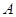 和
和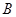 开始有交点;
开始有交点;
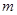 增大到约0.6,又出现直线和圆相切,此后两条直线所夹的部分恰好穿过圆环内部,仍有交点;
增大到约0.6,又出现直线和圆相切,此后两条直线所夹的部分恰好穿过圆环内部,仍有交点;
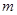 增大到约1,又出现直线和圆相切,此后两条直线所夹的部分和圆环有交点;
增大到约1,又出现直线和圆相切,此后两条直线所夹的部分和圆环有交点;
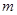 增大到约3.4,又出现直线和圆相切,此后两条直线和圆环相离,没有交点;
增大到约3.4,又出现直线和圆相切,此后两条直线和圆环相离,没有交点;
因此,根据圆心到直线的距离可以算出临界值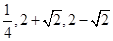 ,又因为
,又因为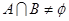 ,所以集合
,所以集合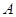 不能使空集,所以
不能使空集,所以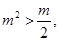 所以
所以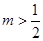 ,所以实数
,所以实数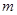 的取值范围是
的取值范围是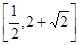 .
.
考点:本小题主要考查直线与圆的位置关系的灵活应用,考查学生数形结合思想的应用和转化问题的能力.
点评:解决此题时要注意充分利用数形结合的思想,另外还要注意因为集合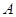 不能是空集,所以
不能是空集,所以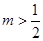 ,所以虽然
,所以虽然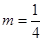 时,也出现了圆环,但并不是集合
时,也出现了圆环,但并不是集合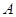 表示的图形。
表示的图形。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com