
【题目】已知直线l1:mx+8y+n=0与l2:2x+my-1=0互相平行,且l1,l2之间的距离为![]() ,求直线l1的方程.
,求直线l1的方程.
【答案】见解析
【解析】试题分析:当两条直线的斜率存在时,两条直线平行只需斜率相等截距不等,当两条直线的斜率均不存在时,两条直线平行,当一条直线斜率不存在而另一条直线斜率存在,两条直线不平行;两条平行线间的距离可用两条平行线间的距离公式去求,但使用公式时要化为一般式,且x, y的系数一致.
试题解析:
∵l1∥l2,∴ ![]() ,
,
∴![]() 或
或![]() ,
,
(1)当m=4时,直线l1的方程为4x+8y+n=0,
把l2的方程写成4x+8y-2=0,
∴![]() ,解得n=-22或n=18.
,解得n=-22或n=18.
故所求直线的方程为2x+4y-11=0或2x+4y+9=0.
(2)当m=-4时,直线l1的方程为4x-8y-n=0,
l2的方程为2x-4y-1=0,
∴![]() ,解得n=-18或n=22.
,解得n=-18或n=22.
故所求直线的方程为2x-4y+9=0或2x-4y-11=0.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知点 ![]() 及圆
及圆 ![]() .
.
(1)设过点 ![]() 的直线
的直线 ![]() 与圆
与圆 ![]() 交于
交于 ![]() 两点,当
两点,当 ![]() 时,求以线段
时,求以线段 ![]() 为直径的圆
为直径的圆 ![]() 的方程;
的方程;
(2)设直线 ![]() 与圆
与圆 ![]() 交于
交于 ![]() 两点,是否存在实数
两点,是否存在实数 ![]() ,使得过点
,使得过点 ![]() 的直线
的直线 ![]() 垂直平分弦
垂直平分弦 ![]() ?若存在,求出实数
?若存在,求出实数 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )

A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车租赁公司为了调查A,B两种车型的出租情况,现随机抽取了这两种车型各100辆汽车,分别统计了每辆车某个星期内的出租天数,统计数据如下表: A型车
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
B型车
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
( I)从出租天数为3天的汽车(仅限A,B两种车型)中随机抽取一辆,估计这辆汽车恰好是A型车的概率;
(Ⅱ)根据这个星期的统计数据,估计该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率;
(Ⅲ)如果两种车型每辆车每天出租获得的利润相同,该公司需要从A,B两种车型中购买一辆,请你根据所学的统计知识,给出建议应该购买哪一种车型,并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣k(
﹣k( ![]() +lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为( )
+lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为( )
A.(﹣∞,e]
B.[0,e]
C.(﹣∞,e)
D.[0,e)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,一个焦点F(﹣2,0),且长轴长与短轴长的比是 ![]() .
.
(1)求椭圆C的方程;
(2)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点.当 ![]() 最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AB=AA1=1,E为BC中点. 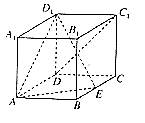
(1)求证:C1D⊥D1E;
(2)若二面角B1﹣AE﹣D1的大小为90°,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,AD⊥AF,AE=AD=2. (Ⅰ)证明:平面PAD⊥平面ABFE;
(Ⅱ)求正四棱锥P﹣ABCD的高h,使得二面角C﹣AF﹣P的余弦值是 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com