
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于4?若存在,求出直线l的方程;若不存在,请说明理由.
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练15练习卷(解析版) 题型:解答题
设椭圆 =1(a>b>0)的左焦点为F,离心率为
=1(a>b>0)的左焦点为F,离心率为 ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为 .
.
(1)求椭圆的方程;
(2)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若 +
+ =8,求k的值.
=8,求k的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:选择题
已知m和n是两条不同的直线,α和β是两个不重合的平面,那么下面给出的条件中一定能推出m⊥β的是( ).
A.α⊥β,且m?α B.m∥n,且n⊥β
C.α⊥β,且m∥α D.m⊥n,且n∥β
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:填空题
设Sn为数列{an}的前n项和,若 (n∈N*)是非零常数,则称该数列为“和等比数列”;若数列{cn}是首项为2,公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,则d=________.
(n∈N*)是非零常数,则称该数列为“和等比数列”;若数列{cn}是首项为2,公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,则d=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:选择题
数列{an}的通项公式an= ,若{an}前n项和为24,则n为( ).
,若{an}前n项和为24,则n为( ).
A.25 B.576 C.624 D.625
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:选择题
已知点P(x,y)是直线kx+y+4=0(k>0)上一动点,PA,PB是圆C:x2+y2-2y=0的两条切线,A,B为切点,若四边形PACB的最小面积是2,则k的值为( ).
A.4 B.3 C.2 D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:选择题
已知过A(-1,a),B(a,8)两点的直线与直线2x-y+1=0平行,则a的值为( ).
A.-10 B.17 C.5 D.2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(解析版) 题型:解答题
已知等差数列{an}满足:a2=5,a4+a6=22,数列{bn}满足b1+2b2+…
+2n-1bn=nan,设数列{bn}的前n项和为Sn.
(1)求数列{an},{bn}的通项公式;
(2)求满足13<Sn<14的n的集合.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(解析版) 题型:选择题
甲射击命中目标的概率是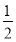 ,乙命中目标的概率是
,乙命中目标的概率是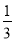 ,丙命中目标的概率是
,丙命中目标的概率是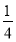 .现在三人同时射击目标,则目标被击中的概率为( ).
.现在三人同时射击目标,则目标被击中的概率为( ).
A.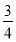 B.
B.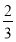 C.
C.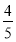 D.
D. 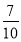
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com