
分析 把函数解析式变形,利用基本不等式求出函数的最值判断①;
运用等差数列的通项公式和等比数列的性质,即可求得公比,进而判断②;
运用1的代换,化简整理运用基本不等式即可求得最小值,即可判断③;
首先利用换元法设出区域B内点的坐标,再根据区域A内点的约束条件求出区域B内点的约束条件,然后画出其可行域,最后由三角形面积公式求得面积判断④.
解答 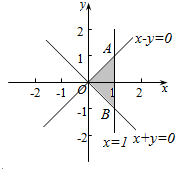 解:①函数y=$\frac{{x}^{2}-x+4}{x-1}(x>1)$=$\frac{(x-1)^{2}+(x-1)+4}{x-1}$=$(x-1)+\frac{4}{x-1}+1$$≥2\sqrt{(x-1)•\frac{4}{x-1}}+1=5$,
解:①函数y=$\frac{{x}^{2}-x+4}{x-1}(x>1)$=$\frac{(x-1)^{2}+(x-1)+4}{x-1}$=$(x-1)+\frac{4}{x-1}+1$$≥2\sqrt{(x-1)•\frac{4}{x-1}}+1=5$,
当且仅当x=3时上式等号成立,∴函数y=$\frac{{x}^{2}-x+4}{x-1}(x>1)$的最小值为5,则①正确;
②等差数列{an}中,a1,a3,a4成等比数列,则有a32=a1a4,即有(a1+2d)2=a1(a1+3d),
解得a1=-4d或d=0,则公比为$\frac{{a}_{3}}{{a}_{1}}$=1或$\frac{1}{2}$,则②错误;
等差数列{an}中,a1,a3,a4成等比数列,则公比为$\frac{1}{2}$;
③由于a>0,b>0,a+b=1,则$\frac{2}{a}+\frac{3}{b}$=(a+b)($\frac{2}{a}+\frac{3}{b}$)=5+$\frac{2b}{a}+\frac{3a}{b}$≥5+2$\sqrt{\frac{2b}{a}•\frac{3a}{b}}$=5+2$\sqrt{6}$,
当且仅当$\sqrt{2}$b=$\sqrt{3}$a时取得最小值,且为5+2$\sqrt{6}$,则③正确;
④设$\left\{\begin{array}{l}{x′=x+y}\\{y′=x-y}\end{array}\right.$,则$\left\{\begin{array}{l}{x=\frac{x′+y′}{2}}\\{y=\frac{x′-y′}{2}}\end{array}\right.$,又x+y≤1,且x≥0,y≥0,
解得x′≤1,x′+y′≥0,x′-y′≥0,即x≤1,x+y≥0,x-y≥0.
画出可行域,如图所示
解得A(1,1)、B(1,-1),
∴S△OAB=$\frac{1}{2}$×2×1=1,即平面区域B的面积为1,则④正确.
故答案为:①③④.
点评 本题考查命题的真假判断与应用,考查基本不等式的运用:求最值,考查等差数列和等比数列的通项和性质,考查运算能力,属于中档题,也是易错题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
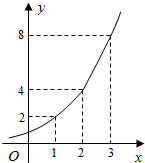 如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述:
如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述:| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}+\frac{1}{2π}$ | B. | $\frac{1}{4}-\frac{1}{2π}$ | C. | $\frac{1}{2}-\frac{1}{π}$ | D. | $\frac{1}{2}+\frac{1}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com